
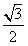 。
。 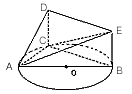
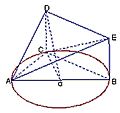
| (Ⅰ)證明:∵四邊形DCBE為平行四邊形, ∴CD∥BE,BC∥DE, ∵DC⊥平面ABC,BC 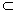 平面ABC, 平面ABC,∴DC⊥BC, ∵AB是圓O的直徑, ∴BC⊥AC且DC∩AC=C, ∴BC⊥平面ADC, ∵DE∥BC,∴DE⊥平面ADC, 又∵DE 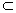 平面ADE, 平面ADE,∴平面ACD⊥平面ADE。 (Ⅱ)解:∵DC⊥平面ABC, ∴BE⊥平面ABC, ∴∠EAB為AE與平面ABC所成的角,即∠EAB =θ, 在Rt△ABE中,由 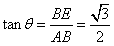 ,AB=2得 ,AB=2得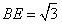 , ,在Rt△ABC中, ∵ 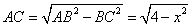 (0<x<2), (0<x<2),∴ 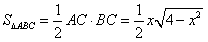 , ,∴  (0<x<2)。 (0<x<2)。 |
|
|
(Ⅲ)解:由(Ⅱ)知0<x<2, |
 |


科目:高中數學 來源: 題型:
 如圖,△ABC內接于圓O,AB是圓O的直徑,AB=2,BC=1,設AE與平面ABC所成的角為θ,且tanθ=
如圖,△ABC內接于圓O,AB是圓O的直徑,AB=2,BC=1,設AE與平面ABC所成的角為θ,且tanθ=
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
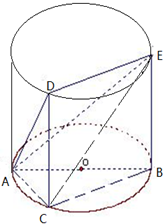 如圖,△ABC內接于圓柱的底面圓O,AB是圓O的直徑,AB=2,BC=1,DC、EB是兩條母線,且 tan∠EAB=
如圖,△ABC內接于圓柱的底面圓O,AB是圓O的直徑,AB=2,BC=1,DC、EB是兩條母線,且 tan∠EAB=
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
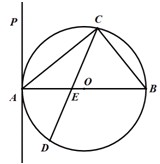 (2013•沈陽二模)選修4-1:幾何證明選講
(2013•沈陽二模)選修4-1:幾何證明選講查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com