
已知函數![]() .
.
(Ⅰ) 當![]() 時,求函數
時,求函數![]() 的單調區間和極值;
的單調區間和極值;
(Ⅱ) 若![]() 在
在![]() 上是單調增函數,求實數a的取值范圍.
上是單調增函數,求實數a的取值范圍.
解析: (Ⅰ) 易知,函數![]() 的定義域為
的定義域為![]() . ………………………1分w.w.w.k.s.5.u.c.o.m
. ………………………1分w.w.w.k.s.5.u.c.o.m ![]()
當![]() 時,
時,![]() . ………………………3分
. ………………………3分
當x變化時,![]() 和
和![]() 的值的變化情況如下表:
的值的變化情況如下表:
x | (0,1) | 1 | (1,+∞) |
| - | 0 | + |
| 遞減 | 極小值 | 遞增 |
………………………5分
由上表可知,函數![]() 的單調遞減區間是(0,1)、單調遞增區間是(1,+∞)、極小值是
的單調遞減區間是(0,1)、單調遞增區間是(1,+∞)、極小值是![]() . ………………………7分w.w.w.k.s.5.u.c.o.m
. ………………………7分w.w.w.k.s.5.u.c.o.m ![]()
(Ⅱ) 由![]() ,得
,得![]() . ………………………9分
. ………………………9分
若函數![]() 為
為![]() 上的單調增函數,則
上的單調增函數,則![]() 在
在![]() 上恒成立,即不等式
上恒成立,即不等式![]() 在
在![]() 上恒成立.也即
上恒成立.也即![]() 在
在![]() 上恒成立. ………11分
上恒成立. ………11分
令![]() ,則
,則![]() . w.w.w.k.s.5.u.c.o.m
. w.w.w.k.s.5.u.c.o.m ![]()
當![]() 時,
時,![]() ,
,![]() 在
在![]() 上為減函數,
上為減函數,
![]() . ………………………………………………13分
. ………………………………………………13分
所以![]() .
.
∴![]() 的取值范圍為
的取值范圍為![]() . ………………………14分
. ………………………14分


科目:高中數學 來源: 題型:
已知函數![]() (1)當a=4,
(1)當a=4,![]() ,求函數f(x)的最大值;(2)若x≥a , 試求f(x)+3 >0 的解集;(3)當
,求函數f(x)的最大值;(2)若x≥a , 試求f(x)+3 >0 的解集;(3)當![]() 時,f(x)≤2x – 2 恒成立,求實數a的取值范圍.
時,f(x)≤2x – 2 恒成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山東省濟寧市泗水一中高三(上)期末數學模擬試卷(理科)(解析版) 題型:選擇題
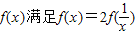 ,當x∈[1,3]時,f(x)=lnx,若在區間
,當x∈[1,3]時,f(x)=lnx,若在區間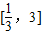 內,函數g(x)=f(x)-ax,有三個不同的零點,則實數a的取值范圍是( )
內,函數g(x)=f(x)-ax,有三個不同的零點,則實數a的取值范圍是( )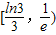
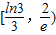
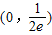
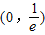
查看答案和解析>>
科目:高中數學 來源:2011-2012學年福建省晉江市四校高三第二次聯合考試文科數學試卷 題型:選擇題
已知函數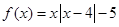 ,則當方程
,則當方程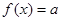 有三個不同實根時,實數
有三個不同實根時,實數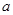 的取值范圍
是 ( )
的取值范圍
是 ( )
A. B.
B.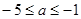 C.
C.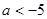 D.
D.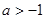
查看答案和解析>>
科目:高中數學 來源:2011-2012年山東省濟寧市高二上學期期中考試文科數學 題型:解答題
(本小題滿分12分)
已知函數f(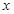 )=
)= ,當
,當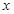 ∈(-2,6)時,其值為正,而當
∈(-2,6)時,其值為正,而當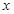 ∈(-∞,-2)∪(6,+∞)時,其值為負
∈(-∞,-2)∪(6,+∞)時,其值為負
(I)
求實數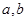 的值及函數f(
的值及函數f(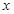 )的解析式
)的解析式
(II)設F(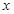 )= -
)= -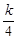 f(
f(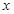 )+4
)+4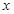 +12
+12 ,問
,問 取何值時,方程F(
取何值時,方程F(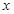 )=0有正根?
)=0有正根?
查看答案和解析>>
科目:高中數學 來源:2010年重慶市高一上學期期中考試數學試題 題型:解答題
(本小題滿分10分)
已知函數 ,當點 (x,y)
是函數y = f (x) 圖象上的點時,點
,當點 (x,y)
是函數y = f (x) 圖象上的點時,點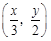 是函數y =
g(x) 圖象上的點.
是函數y =
g(x) 圖象上的點.
(1) 寫出函數y = g (x) 的表達式;
(2)
當g(x)-f (x)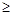 0時,求x的取值范圍;
0時,求x的取值范圍;
(3)
當x在 (2) 所給范圍內取值時,求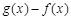 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com