
 ,2an+1=f(an)+15,bn=
,2an+1=f(an)+15,bn=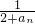 (n∈N+).已知不等式|f(x)≤2x2+4x-30|對任意實數x均成立.
(n∈N+).已知不等式|f(x)≤2x2+4x-30|對任意實數x均成立. )n]≤Sn<2.
)n]≤Sn<2.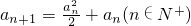 ,
,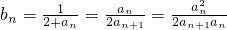 =
=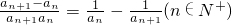 ,
,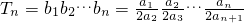 =
=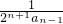 ,(n∈N+),
,(n∈N+),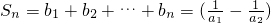
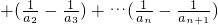
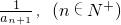 .
.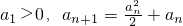 ,
,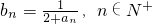 ,
,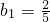 .
.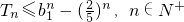 ,
,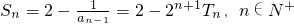 ,
, )n]≤Sn<2.
)n]≤Sn<2.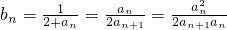 =
=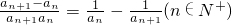 ,
,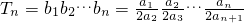 =
=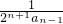 ,(n∈N+),由此能夠證明對任意n∈N+,有2n+1Tn+Sn為定值.
,(n∈N+),由此能夠證明對任意n∈N+,有2n+1Tn+Sn為定值.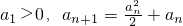 ,知{an}為單調遞增的正數數列,由
,知{an}為單調遞增的正數數列,由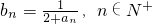 ,知{bn}為單調遞減的正數數列,且
,知{bn}為單調遞減的正數數列,且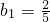 .由此能夠證明對任意正整數n,都有2[1-(
.由此能夠證明對任意正整數n,都有2[1-( )n]≤Sn<2.
)n]≤Sn<2.

 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:
| 1 | x+1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| n+1 |
| n |
| n-1 |
| n3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com