某城市理論預測2000年到2005年人口總數與年份的關系如下表所示
(1) 畫出散點圖，試建立y與x之間的回歸方程.
(2) 據此估計2006年人口總數.
(3) 計算相關指數
、殘差、殘差平方和.
| 年份x | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| 人口數y萬 | 50 | 69 | 88 | 110 | 190 | 350 |
見解析
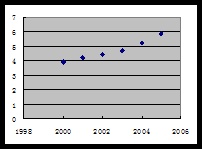
解：(1) 散點圖如右圖所示：
由圖知，樣本點分布在某一條指數函數曲線
的周圍，令z=lny，
則
得到變換后的數據如下表：
| x | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 |
| z | 3.912 | 4.234 | 4.477 | 4.700 | 5.247 | 5.858 |
作散點圖如下右圖所示，即知變換后的樣本分布在一條直線附近，故可以用線性回歸方程來擬合由計算器計算得線性回歸方程為 
，因此，年份x與人口數y萬之間的非線性回歸方程為
.
(2) 估計2006年人口總數應為418.759萬
(3) 相關指數
| 年份x | 人口數y（萬） |
|
|
| 2000 | 50 | 45.159 | 4.841 |
| 2001 | 69 | 65.456 | 3.544 |
| 2002 | 88 | 94.875 | -6.875 |
| 2003 | 110 | 137.516 | -27.516 |
| 2004 | 190 | 199.323 | -9.323 |
| 2005 | 350 | 288.909 | 61.091 |
即知殘差平方和為4659.420.
學而優銜接教材南京大學出版社系列答案科目：高中數學 來源： 題型：
| 年份200x（年） | 0 | 1 | 2 | 3 | 4 |
| 人口數y（十）萬 | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目：高中數學 來源： 題型：
| 年份200x（年） | 0 | 1 | 2 | 3 | 4 |
| 人口數y（十）萬 | 5 | 7 | 8 | 11 | 19 |
查看答案和解析>>
科目：高中數學 來源：2013屆福建省高二下學期期中文科數學試卷（解析版） 題型：解答題
（本小題滿分10分）
某城市理論預測2000年到2004年人口總數與年份的關系如下表所示
|
年份200x（年） |
0 |
1 |
2 |
3 |
4 |
|
人口數 y （十萬） |
5 |
7 |
8 |
11 |
19 |
（Ⅰ）請畫出上表數據的散點圖；
（Ⅱ）請根據上表提供的數據，用最小二乘法求出 y 關于x的線性回歸方程；
（Ⅲ）據此估計2005年該城市人口總數。
參考數值：0×5+1×7+2×8+3×11+4×19=132，
，
參考公式： 用最小二乘法求線性回歸方程系數公式 
查看答案和解析>>
科目：高中數學 來源：2013屆山西省高二下學期期中考試文科數學試卷（解析版） 題型：填空題
某城市理論預測2000年到2004年人口總數與年份的關系如下表所示
|
年份200x（年） |
0 |
1 |
2 |
3 |
4 |
|
人口數 y （十萬） |
5 |
7 |
8 |
11 |
19 |
根據表格和線性回歸方程，可預報在2005年，該城市人口總數是___________
( 參考數值：0×5+1×7+2×8+3×11+4×19=132，
，公式見卷首 )
查看答案和解析>>
科目：高中數學 來源：2013屆河南省高二3月月考文科數學試卷 題型：解答題
某城市理論預測2000年到2004年人口總數與年份的關系如下表所示
|
年份200x（年） |
0 |
1 |
2 |
3 |
4 |
|
人口數y（十）萬 |
5 |
7 |
8 |
11 |
19 |
(1)請畫出上表數據的散點圖；
(2)請根據上表提供的數據，求出Y關于x的線性回歸方程Y=bx+a；
(3)據此估計2005年.該 城市人口總數。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
