已知函數f(x)＝
的圖象過原點，且關于點(－1,2)成中心對稱．
(1)求函數f(x)的解析式；
(2)若數列{an}滿足a1＝2，an＋1＝f(an)，試證明數列
為等比數列，并求出數列{an}的通項公式．
考前必練系列答案科目：高中數學 來源： 題型：解答題
已知函數f(x)=-x+log2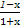
.
(1)求f(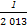
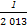)+f(-)的值.
(2)當x∈(-a,a],其中a∈(0,1),a是常數時,函數f(x)是否存在最小值?若存在,求出f(x)的最小值;若不存在,請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
如果對任意實數x,y,都有f(x+y)=f(x)·f(y),且f(1)=2,
(1)求f(2),f(3),f(4)的值.
(2)求
+
+
+…+
+
+
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
某興趣小組要測量電視塔AE的高度H(單位：m)．如示意圖，垂直放置的標桿BC的高度h＝4 m，仰角∠ABE＝α，∠ADE＝β.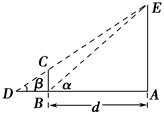
(1)該小組已測得一組α，β的值，算出了tan α＝1.24，tan β＝1.20，請據此算出H的值；
(2)該小組分析若干測得的數據后，認為適當調整標桿到電視塔的距離d(單位：m)，使α與β之差較大，可以提高測量精度．若電視塔的實際高度為125 m，試問d為多少時，α－β最大？
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
經市場調查，某旅游城市在過去的一個月內(以30天計)，旅游人數f(t)(萬人)與時間t(天)的函數關系近似滿足f(t)＝4＋
，人均消費g(t)(元)與時間t(天)的函數關系近似滿足g(t)＝115－|t－15|.
(1)求該城市的旅游日收益w(t)(萬元)與時間t(1≤t≤30，t∈N*)的函數關系式；
(2)求該城市旅游日收益的最小值(萬元)．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝
，x∈[－1,1]，函數g(x)＝[f(x)]2－2af(x)＋3的最小值為h(a)．
(1)求h(a)；
(2)是否存在實數m、n同時滿足下列條件：
①m＞n＞3；
②當h(a)的定義域為[n，m]時，值域為[n2，m2]？若存在，求出m、n的值；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
若函數f(x)對任意的實數x1，x2∈D，均有|f(x2)－f(x1)|≤|x2－x1|，則稱函數f(x)是區間D上的“平緩函數”．
(1)判斷g(x)＝sin x和h(x)＝x2－x是不是實數集R上的“平緩函數”，并說明理由；
(2)若數列{xn}對所有的正整數n都有|xn＋1－xn|≤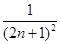
，設yn＝sin xn，求證：|yn＋1－y1|＜
.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
上海某化學試劑廠以x千克/小時的速度生產某種產品（生產條件要求
），為了保證產品的質量，需要一邊生產一邊運輸，這樣按照目前的市場價格，每小時可獲得利潤是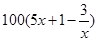
元.
(1)要使生產運輸該產品2小時獲得的利潤不低于3000元，求x的取值范圍；
(2)要使生產運輸900千克該產品獲得的利潤最大，問：該工廠應該選取何種生產速度？并求最大利潤.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
（2）an＝
[3(x＋1)]圖．