
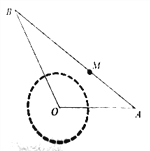
【題目】某綜藝頻道舉行某個水上娛樂游戲,如圖,固定在水面上點![]() 處的某種設備產生水波圈,水波圈生產
處的某種設備產生水波圈,水波圈生產![]() 秒時的半徑
秒時的半徑![]() (單位:
(單位: ![]() )滿足
)滿足![]() ;
; ![]() 是鋪設在水面上的浮橋,浮橋的寬度忽略不計,浮橋兩端
是鋪設在水面上的浮橋,浮橋的寬度忽略不計,浮橋兩端![]() 固定在水岸邊.游戲規定:當點
固定在水岸邊.游戲規定:當點![]() 處剛產生水波圈時,游戲參與者(視為一個點)與此同時從浮橋的
處剛產生水波圈時,游戲參與者(視為一個點)與此同時從浮橋的![]() 端跑向
端跑向![]() 端;若該參與者通過浮橋
端;若該參與者通過浮橋![]() 的過程中,從點
的過程中,從點![]() 處發出的水波圈始終沒能到達此人跑動時的位置,則認定該參與者在這個游戲中過關;否則認定在這個游戲中不過關,已知
處發出的水波圈始終沒能到達此人跑動時的位置,則認定該參與者在這個游戲中過關;否則認定在這個游戲中不過關,已知![]() ,
, ![]() ,浮橋
,浮橋![]() 的某個橋墩處點
的某個橋墩處點![]() 到直線
到直線![]() 的距離分別為
的距離分別為![]() ,且
,且![]() ,若某游戲參與者能以
,若某游戲參與者能以![]() 的速度從浮橋
的速度從浮橋![]() 端勻速跑到
端勻速跑到![]() 端.
端.
(1)求該游戲參與者從浮橋![]() 端跑到
端跑到![]() 端所需的時間?
端所需的時間?
(2)問該游戲參與者能否在這個游戲中過關?請說明理由.
【答案】(1)![]() ;(2)見解析.
;(2)見解析.
【解析】試題分析:(1)設![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() (舍).求得直線
(舍).求得直線![]() 的方程為
的方程為![]() ,與
,與![]() 聯立可得
聯立可得![]() ,求得AB,進而可得所需時間;
,求得AB,進而可得所需時間;
(2)求得![]() 時,點
時,點![]() 坐標為
坐標為![]() ,其中
,其中![]() .
. ![]() ,
, ![]() .構造函數
.構造函數![]()
![]() ,求導計算可得
,求導計算可得![]() 時,
時, ![]() 恒成立,所以該參與者在這個游戲中過關.
恒成立,所以該參與者在這個游戲中過關.
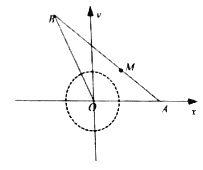
試題解析:(1)建立如圖所示的直角坐標系,則![]() ,
,
直線![]() 的方程為
的方程為![]() .
.
設![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() .
.
當![]() 時,
時, ![]() ,符合;
,符合;
當![]() 時,
時, ![]() ,不符合.
,不符合.
所以![]() ,直線
,直線![]() 的方程為
的方程為![]() .
.
由![]() 解得
解得![]() 即
即![]() .
.
所以![]() .
.
所以,該游戲參與者從浮橋![]() 端跑到
端跑到![]() 端所需的時間為
端所需的時間為![]() .
.
(2)在![]() 中,
中, ![]() ,
, ![]() .
.
設![]() 時,該參與者位于點
時,該參與者位于點![]() ,則
,則![]() ,
, ![]() .
.
則![]() 時,點
時,點![]() 坐標為
坐標為![]() ,其中
,其中![]() .
.
![]() ,
, ![]() .
.
令![]()
![]() ,
,
則![]()
![]()
![]() 時
時![]() ,
, ![]() 在
在![]() 上為增函數,
上為增函數,
![]() 時
時![]() ,
, ![]() 在
在![]() 上為減函數,
上為減函數,
故當![]() 時,
時, ![]() 取得最大值
取得最大值![]() .
.
由于![]() ,所以
,所以![]() 時,
時, ![]() 恒成立.
恒成立.
即該游戲參與者通過浮橋![]() 的過程中,從點
的過程中,從點![]() 處發出的水波圈始終沒能到達此人跑動時的位置,所以該參與者在這個游戲中過關.
處發出的水波圈始終沒能到達此人跑動時的位置,所以該參與者在這個游戲中過關.
點晴:本題考查的是函數模型的應用。解決函數模型應用的解答題,要注意以下幾點:①讀懂實際背景,將實際問題轉化為函數模型.②對涉及的相關公式,記憶要準確.③在求解的過程中計算要正確.另外需要熟練掌握求解方程、不等式、函數最值的方法,才能快速正確地求解.


科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點, ![]() 軸的正半軸為極軸,以相同的長度單位建立極坐標系,已知直線
軸的正半軸為極軸,以相同的長度單位建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)設![]() 為參數,若
為參數,若![]() ,求直線
,求直線![]() 的參數方程;
的參數方程;
(2)已知直線![]() 與曲線
與曲線![]() 交于
交于![]() ,設
,設![]() ,且
,且![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】解答
(1)將一顆骰子(一種各個面上分別標有1,2,3,4,5,6個點的正方體玩具)先后拋擲2次,以分別得到的點數(m,n)作為點P的坐標(m,n),求:點P落在區域 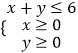 內的概率;
內的概率;
(2)在區間[1,6]上任取兩個實數(m,n),求:使方程x2+mx+n2=0有實數根的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
以直角坐標系的原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立坐標系,已知點
軸的正半軸為極軸建立坐標系,已知點![]() 的直角坐標為
的直角坐標為![]() ,若直線
,若直線![]() 的極坐標方程為
的極坐標方程為![]() .曲線
.曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數).
為參數).
(1)求直線![]() 和曲線
和曲線![]() 的普通方程;
的普通方程;
(2)設直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人參加某種選拔測試,在備選的10道題中,甲答對其中每道題的概率都是![]() ,乙能答對其中的5道題。規定每次考試都從備選的10道題中隨機抽出3道題進行測試,答對一題加10分,答錯一題(不答視為答錯)減5分,至少得15分才能入選.
,乙能答對其中的5道題。規定每次考試都從備選的10道題中隨機抽出3道題進行測試,答對一題加10分,答錯一題(不答視為答錯)減5分,至少得15分才能入選.
(I)求甲能入選的概率.
(II)求乙得分的分布列和數學期望;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sin(ωx+φ)(ω>0,|φ|< ![]() )的部分圖象如圖所示.
)的部分圖象如圖所示.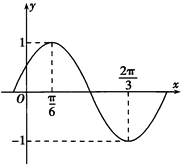
(1)求函數f(x)的解析式,并寫出f(x)的單調減區間;
(2)已知△ABC的內角分別是A,B,C,A為銳角,且f ![]() ,求cosA的值.
,求cosA的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,a、b、c分別是角A、B、C的對邊,如果a,b,c成等差數列,B=60°,△ABC的面積為3 ![]() ,那么b等于( )
,那么b等于( )
A.2 ![]()
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設Sn為正項數列{an}的前n項和,a1=2,Sn+1(Sn+1﹣2Sn+1)=3Sn(Sn+1),則a100等于( )
A.2×398
B.4×398
C.2×399
D.4×399
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com