
如圖,在四棱錐P-ABCD中,底面ABCD為菱形,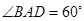 ,Q為AD的中點.
,Q為AD的中點.

(1)若PA=PD,求證:平面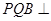 平面PAD;
平面PAD;
(2)點M在線段上,PM=tPC,試確定實數t的值,使PA//平面MQB.
(1)見解析(2)
解析試題分析:
(1)要證明平面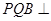 平面PAD,根據面面垂直的定義,只需要在面PAD中找到一條直線AD垂直于面PQB即可,根據三角形PAD為等腰三角形且Q為中點,三線合一即可得到PQ垂直于AD,再利用底面四邊形ABCD為菱形且有個角為60度即可得到三星ABD為等邊三角形,再次利用等腰三角形的三線合一即可證明QB垂直于AD,則AD垂直于面PQB內兩條相交的線段QB與PQ,即可得到AD垂直于面PQB,即有面面垂直.
平面PAD,根據面面垂直的定義,只需要在面PAD中找到一條直線AD垂直于面PQB即可,根據三角形PAD為等腰三角形且Q為中點,三線合一即可得到PQ垂直于AD,再利用底面四邊形ABCD為菱形且有個角為60度即可得到三星ABD為等邊三角形,再次利用等腰三角形的三線合一即可證明QB垂直于AD,則AD垂直于面PQB內兩條相交的線段QB與PQ,即可得到AD垂直于面PQB,即有面面垂直.
(2)連 交
交 于
于 ,根據線面平行的性質定理,可以得到
,根據線面平行的性質定理,可以得到 ,則在三角形PAC與三角形MNC中,有一組邊平行,則兩個三角形相似,則有
,則在三角形PAC與三角形MNC中,有一組邊平行,則兩個三角形相似,則有 ,利用底面是有個角為60度的菱形和Q為中點可以求的
,利用底面是有個角為60度的菱形和Q為中點可以求的 ,即可得到
,即可得到 .
.
試題解析:
(1)連結 ,因為四邊形
,因為四邊形 為菱形,
為菱形,
且 ,所以
,所以 為正三角形,
為正三角形,
又 為
為 的中點,所以
的中點,所以 ; 2分
; 2分
又因為 ,Q為AD的中點,所以
,Q為AD的中點,所以 .
.
又 ,所以
,所以 4分
4分
又 ,所以
,所以 6分
6分
(2)證明:因為 平面
平面 ,連
,連 交
交 于
于 ,
,
由 可得,
可得, ∽
∽ ,所以
,所以 , 8分
, 8分
因為 平面
平面 ,
, 平面
平面 ,平面
,平面
 平面
平面
 .
.
所以 , 10分
, 10分
因此, .即
.即 的值為
的值為 . 12分
. 12分

考點:線面平行的性質定理面面垂直三線合一


科目:高中數學 來源: 題型:解答題
如圖所示,在四棱錐P-ABCD中,AB⊥平面PAD,AB∥CD,PD=AD,E是PB的中點,F是DC上的點且DF= AB,PH為△PAD邊上的高.
AB,PH為△PAD邊上的高.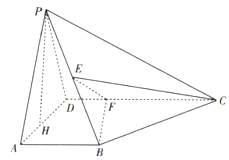
(1)證明:PH⊥平面ABCD;
(2)若PH=1,AD=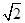 ,FC=1,求三棱錐E-BCF的體積;
,FC=1,求三棱錐E-BCF的體積;
(3)證明:EF⊥平面PAB.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知三棱錐P-ABC中,∠ACB=90°,CB=4,AB=20,D為AB中點,M為PB中點,且△PDB是正三角形,PA⊥PC。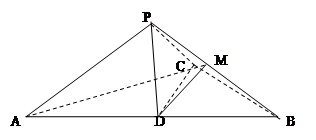 .
.
(1)求證:DM∥平面PAC;
(2)求證:平面PAC⊥平面ABC;
(3)求三棱錐M-BCD的體積
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,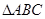 在平面
在平面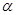 內,
內,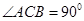 ,AB=2BC=2,P為平面
,AB=2BC=2,P為平面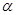 外一個動點,且PC=
外一個動點,且PC=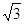 ,
,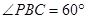
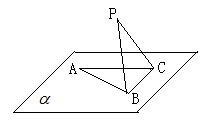
(1)問當PA的長為多少時,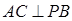
(2)當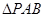 的面積取得最大值時,求直線PC與平面PAB所成角的正弦值
的面積取得最大值時,求直線PC與平面PAB所成角的正弦值
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在四棱錐P-ABCD中,AB∥DC,AB⊥平面PAD, PD=AD,AB=2DC,E是PB的中點.
求證:(1)CE∥平面PAD;
(2)平面PBC⊥平面PAB.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,四棱錐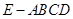 ,底面
,底面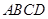 是矩形,平面
是矩形,平面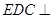 底面
底面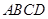 ,
,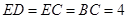 ,
,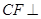 平面
平面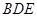 ,且點
,且點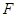 在
在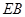 上.
上.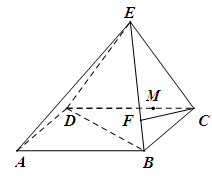
(1)求證: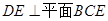 ;
;
(2)求三棱錐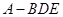 的體積;
的體積;
(3)設點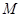 在線段
在線段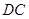 上,且滿足
上,且滿足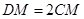 ,試在線段
,試在線段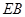 上確定一點
上確定一點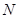 ,使得
,使得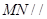 平面
平面 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在三棱錐S ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.過A作AF⊥SB,垂足為F,點E,G分別是棱SA,SC的中點.
ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.過A作AF⊥SB,垂足為F,點E,G分別是棱SA,SC的中點.
求證:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在正方體ABCD-A1B1C1D1中,E、F分別是CD、A1D1中點.
(1)求證:AB1⊥BF;
(2)求證:AE⊥BF;
(3)棱CC1上是否存在點F,使BF⊥平面AEP,若存在,確定點P的位置;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com