為了解某學校高中學生視力的情況,擬采取分層抽樣的方法從高一、高二、高三年級中抽取7個班進行調查,已知該校高一、高二、高三年級分別有8,8,12個班.
(1)從高一、高二、高三年級中應分別抽取多少個班?
(2)若從抽取的7(3)個班中隨機地抽取2(4)個班進行調查結果的對比.求這兩個班都來自高三年級的概率和這兩個班來自不同年級的概率.
【答案】
分析:(1)由題意知總體個數是8+8+12,要抽取的個數是7,做出每個個體被抽到的概率,分別用三個年級的數目乘以概率,得到每一個年級要抽取的班數.
(2)由題意知本題是一個古典概型,從7個班中隨機地抽取2個班共有C
72個等可能的結果,其中這兩個班都來自高三年級的共有C
32個結果,這兩個班來自同年級的共有C
22+C
22+C
32個結果,得到概率.
解答:解:(1)由題意知總體個數是8+8+12,要抽取的個數是7,
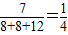
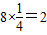
,
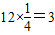
∴從高一、高二、高三年級中應分別抽取2,2,3個班
(2)設A表示事件“這兩個班都來自高三年級”;B表示事件“這兩個班來自不同年級”
從7個班中隨機地抽取2個班共有C
72=21個等可能的結果,
其中這兩個班都來自高三年級的共有C
32=3個結果,
這兩個班來自同年級的共有C
22+C
22+C
32=5個結果,
∴P(A)=
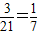
;P(B)=
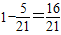 點評:
點評:本題考查分層抽樣,考查古典概型的概率公式,是一個基礎題,可以作為解答題目出現在大型考試中,是一個送分題目.

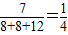
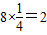 ,
,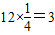
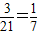 ;P(B)=
;P(B)=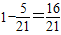


 閱讀快車系列答案
閱讀快車系列答案