
 滿足:對于任意的x1,x2∈[0,1]都有|f(x1)-f(x2)|≤1恒成立,則a的取值范圍是 .
滿足:對于任意的x1,x2∈[0,1]都有|f(x1)-f(x2)|≤1恒成立,則a的取值范圍是 . 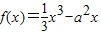 滿足:對于任意的x1,x2∈[0,1],都有|f(x1)-f(x2)|≤1恒成立,必有函數
滿足:對于任意的x1,x2∈[0,1],都有|f(x1)-f(x2)|≤1恒成立,必有函數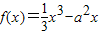 滿足其最大值與最小值的差小于等于1,由此不等式解出參數a的范圍即可,故可先求出函數的導數,用導數判斷出最值,求出最大值與最小值的差,得到關于a的不等式,解出a的值.
滿足其最大值與最小值的差小于等于1,由此不等式解出參數a的范圍即可,故可先求出函數的導數,用導數判斷出最值,求出最大值與最小值的差,得到關于a的不等式,解出a的值. -a2
-a2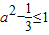 ,解得|a|≤
,解得|a|≤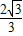 ,解可得
,解可得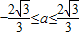 ;
;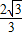 ≤a≤-1或1≤a≤
≤a≤-1或1≤a≤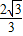 .
.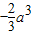 <0,
<0, -a2;
-a2; -a2是最大值,此時也符合,
-a2是最大值,此時也符合,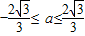 、
、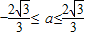 .
.

科目:高中數學 來源:2008-2009學年江蘇省揚州市高三(上)期末數學試卷(解析版) 題型:填空題
 滿足:對于任意的x1,x2∈[0,1]都有|f(x1)-f(x2)|≤1恒成立,則a的取值范圍是 .
滿足:對于任意的x1,x2∈[0,1]都有|f(x1)-f(x2)|≤1恒成立,則a的取值范圍是 .查看答案和解析>>
科目:高中數學 來源:2011-2012學年河南省商丘市虞城高中高三(上)期末數學模擬試卷1(理科)(解析版) 題型:填空題
 滿足:對于任意的x1,x2∈[0,1]都有|f(x1)-f(x2)|≤1恒成立,則a的取值范圍是 .
滿足:對于任意的x1,x2∈[0,1]都有|f(x1)-f(x2)|≤1恒成立,則a的取值范圍是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com