
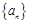 的前n項和為Sn,已知
的前n項和為Sn,已知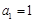 ,且
,且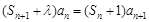 對一切
對一切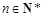 都成立.
都成立.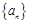 的通項公式;
的通項公式;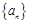 是等差數列.
是等差數列.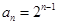 ;(2)
;(2)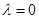 .
.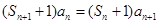 ,我們要從這個式子想辦法得出
,我們要從這個式子想辦法得出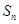 與
與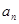 的簡單關系式,變形為
的簡單關系式,變形為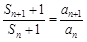 ,這時我們聯想到累乘法求數列通項公式的題型,因此首先由
,這時我們聯想到累乘法求數列通項公式的題型,因此首先由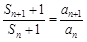 得
得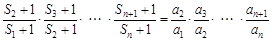 ,又
,又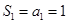 ,這個式子可化簡為
,這個式子可化簡為 ,這樣就變成我們熟悉的已知條件,已知解法了;(2)這種類型問題,一種方法是從特殊到一般的方法,可由
,這樣就變成我們熟悉的已知條件,已知解法了;(2)這種類型問題,一種方法是從特殊到一般的方法,可由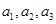 成等差數列,求出
成等差數列,求出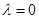 ,然后把
,然后把
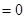 代入已知等式,得
代入已知等式,得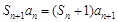 ,
, ,這個等式比第(1)題難度大點,把
,這個等式比第(1)題難度大點,把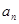 化為
化為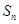 ,有當n≥2時,
,有當n≥2時,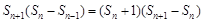 ,整理,得
,整理,得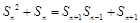 ,特別是可變形為
,特別是可變形為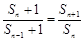 ,這樣與第(1)處理方法相同,可得
,這樣與第(1)處理方法相同,可得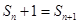 ,即
,即 ,從而說不得
,從而說不得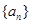 是等差數列.
是等差數列. 試題解析:(1)若λ=1,則
試題解析:(1)若λ=1,則 ,
, .
.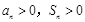 ,∴
,∴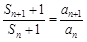 , 2分
, 2分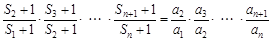 ,
,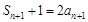 .① 4分
.① 4分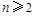 時,
時,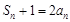 .②
.②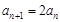 ,∴
,∴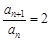 (
(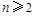 ). 6分
). 6分 ,∴n=1時上式也成立,
,∴n=1時上式也成立,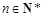 ). 8分
). 8分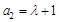 .令n=2,得
.令n=2,得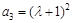 . 10分
. 10分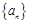 是等差數列,必須有
是等差數列,必須有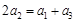 ,解得λ=0. 11分
,解得λ=0. 11分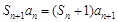 ,且
,且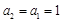 .
.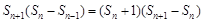 ,
,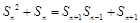 ,
,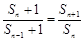 , 13分
, 13分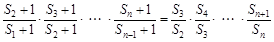 ,
,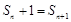 ,所以
,所以 . 15分
. 15分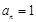 (
(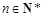 ),
),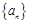 是等差數列. 16分
是等差數列. 16分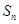 與
與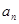 的關系,等差數列.
的關系,等差數列.

 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:高中數學 來源:不詳 題型:解答題
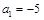 ,
,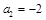 ,記
,記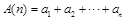 ,
,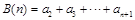 ,
,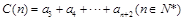 ,若對于任意
,若對于任意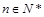 ,A(n),B(n),C(n)成等差數列.
,A(n),B(n),C(n)成等差數列.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.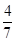 尺 尺 | B.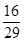 尺 尺 | C.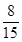 尺 尺 | D.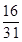 尺 尺 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com