
【題目】已知A,B是橢圓C:![]() )的左右頂點,P點為橢圓C上一點,點P關于x軸的對稱點為H,且
)的左右頂點,P點為橢圓C上一點,點P關于x軸的對稱點為H,且![]()
(1)若橢圓C經過了圓![]() 的圓心,求橢圓C的標準方程;
的圓心,求橢圓C的標準方程;
(2)在(1)的條件下,拋物線D:![]() 的焦點F與點
的焦點F與點![]() 關于y軸上某點對稱,且拋物線D與橢圓C在第四象限交于點Q,過點Q作直線與拋物線D有唯一公共點,求該直線與兩坐標軸圍成的三角形面積.
關于y軸上某點對稱,且拋物線D與橢圓C在第四象限交于點Q,過點Q作直線與拋物線D有唯一公共點,求該直線與兩坐標軸圍成的三角形面積.
科目:高中數學 來源: 題型:
【題目】隨著馬拉松運動在全國各地逐漸興起,參與馬拉松訓練與比賽的人數逐年增加.為此,某市對參加馬拉松運動的情況進行了統計調査,其中一項是調査人員從參與馬拉松運動的人中隨機抽取100人,對其每月參與馬拉松運動訓練的夭數進行統計,得到以下統計表;
平均每月進行訓練的天數 |
|
|
|
人數 | 15 | 60 | 25 |
(1)以這100人平均每月進行訓練的天數位于各區間的頻率代替該市參與馬拉松訓練的人平均每月進行訓練的天數位于該區間的概率.從該市所有參與馬拉松訓練的人中隨機抽取4個人,求恰好有2個人是“平均每月進行訓練的天數不少于20天”的概率;
(2)依據統計表,用分層抽樣的方法從這100個人中抽取12個,再從抽取的12個人中隨機抽取3個,![]() 表示抽取的是“平均每月進行訓練的天數不少于20天”的人數,求
表示抽取的是“平均每月進行訓練的天數不少于20天”的人數,求![]() 的分布列及數學期望
的分布列及數學期望![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,四邊形
中,四邊形![]() ,
,![]() 均為正方形,且
均為正方形,且![]() ,M為
,M為![]() 的中點,N為
的中點,N為![]() 的中點.
的中點.
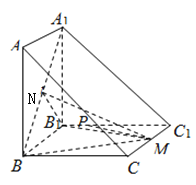
(1)求證:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)設P是棱![]() 上一點,若直線PM與平面
上一點,若直線PM與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 為
為![]() 的直徑,
的直徑,![]() 是弧
是弧![]() 上的一個動點(不與端點
上的一個動點(不與端點![]() 重合),
重合),![]() 為
為![]() 上一點,且
上一點,且![]() 是線段
是線段![]() 上的一個動點(不與端點
上的一個動點(不與端點![]() 重合).
重合).
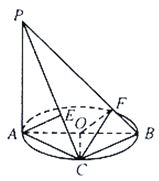
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中點,
的中點,![]() 是銳角,且三棱錐
是銳角,且三棱錐![]() 的體積為
的體積為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的焦點為
的焦點為![]() 和
和![]() ,過
,過![]() 的直線
的直線![]() 交
交![]() 于
于![]() 兩點,過
兩點,過![]() 作與
作與![]() 軸垂直的直線
軸垂直的直線![]() ,又知點
,又知點![]() ,直線
,直線![]() 記為
記為![]() ,
,![]() 與
與![]() 交于點
交于點![]() .設
.設![]() ,已知當
,已知當![]() 時,
時,![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)求證:無論![]() 如何變化,點
如何變化,點![]() 的橫坐標是定值,并求出這個定值.
的橫坐標是定值,并求出這個定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設有限數列![]() ,定義集合
,定義集合![]() 為數列
為數列![]() 的伴隨集合.
的伴隨集合.
(Ⅰ)已知有限數列![]() 和數列
和數列![]() .分別寫出
.分別寫出![]() 和
和![]() 的伴隨集合;
的伴隨集合;
(Ⅱ)已知有限等比數列![]() ,求
,求![]() 的伴隨集合
的伴隨集合![]() 中各元素之和
中各元素之和![]() ;
;
(Ⅲ)已知有限等差數列![]() ,判斷
,判斷![]() 是否能同時屬于
是否能同時屬于![]() 的伴隨集合
的伴隨集合![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com