
【題目】如圖所示,在三棱錐![]() 中,
中,![]() 是邊長為4的正三角形,平面
是邊長為4的正三角形,平面![]() 平面
平面![]() ,SA=SC=
,SA=SC=![]() ,M,N分別為AB,SB的中點.
,M,N分別為AB,SB的中點.
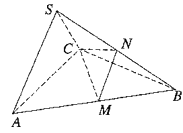
(1)求證:AC⊥SB;
(2)求二面角N-CM-B的余弦值;
科目:高中數學 來源: 題型:
【題目】某超市在節日期間進行有獎促銷,凡在該超市購物滿![]() 元的顧客,將獲得一次摸獎機會,規則如下:一個袋子裝有
元的顧客,將獲得一次摸獎機會,規則如下:一個袋子裝有![]() 只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎勵
只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎勵![]() 元;共兩只球都是綠色,則獎勵
元;共兩只球都是綠色,則獎勵![]() 元;若兩只球顏色不同,則不獎勵.
元;若兩只球顏色不同,則不獎勵.
(1)求一名顧客在一次摸獎活動中獲得![]() 元的概率;
元的概率;
(2)記![]() 為兩名顧客參與該摸獎活動獲得的獎勵總數額,求隨機變量
為兩名顧客參與該摸獎活動獲得的獎勵總數額,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為提高玉米產量,某種植基地對單位面積播種數與每棵作物的產量之間的關系進行了研究,收集了![]() 塊試驗田的數據,得到下表:
塊試驗田的數據,得到下表:
試驗田編號 |
|
|
|
|
|
|
|
|
|
|
|
(棵/) |
|
|
|
|
|
|
|
|
|
|
|
(斤/棵) |
|
|
|
|
|
|
|
|
|
|
|
技術人員選擇模型![]() 作為
作為![]() 與
與![]() 的回歸方程類型,令
的回歸方程類型,令![]() ,
,![]() 相關統計量的值如下表:
相關統計量的值如下表:
|
|
|
|
|
|
|
|
由表中數據得到回歸方程后進行殘差分析,殘差圖如圖所示:

(1)根據殘差圖發現一個可疑數據,請寫出可疑數據的編號(給出判斷即可,不必說明理由);
(2)剔除可疑數據后,由最小二乘法得到關于的線性回歸方程![]() 中的
中的![]() ,求
,求![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(3)利用(2)得出的結果,計算當單位面積播種數![]() 為何值時,單位面積的總產量
為何值時,單位面積的總產量![]() 的預報值最大?(計算結果精確到
的預報值最大?(計算結果精確到![]() )
)
附:對于一組數據![]() ,
,![]() ,
,![]() ,
,![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘法估計分別為
的斜率和截距的最小二乘法估計分別為 ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(13分)設{an}是公比為正數的等比數列a1=2,a3=a2+4.
(Ⅰ)求{an}的通項公式;
(Ⅱ)設{bn}是首項為1,公差為2的等差數列,求數列{an+bn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據市場調查,某種商品一年內每件出廠價在6千元的基礎上,按月呈![]() 的模型波動(x為月份),已知3月份達到最高價8千元,7月份價格最低為4千元,該商品每件的售價為
的模型波動(x為月份),已知3月份達到最高價8千元,7月份價格最低為4千元,該商品每件的售價為![]() (x為月份),且滿足
(x為月份),且滿足![]() .
.
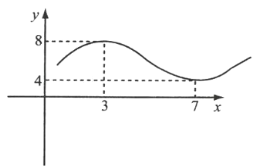
(1)分別寫出該商品每件的出廠價函數![]() 和售價函數
和售價函數![]() 的解析式;
的解析式;
(2)問幾月份的銷售盈利最大?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com