
【題目】下列命題正確的是( )
A.已知隨機變量![]() ,若
,若![]() .則
.則![]()
B.已知分類變量![]() 與
與![]() 的隨機變量
的隨機變量![]() 的觀察值為
的觀察值為![]() ,則當
,則當![]() 的值越大時,“
的值越大時,“![]() 與
與![]() 有關”的可信度越小.
有關”的可信度越小.
C.在線性回歸模型中,計算其相關指數![]() ,則可以理解為:解析變量對預報變量的貢獻率約為
,則可以理解為:解析變量對預報變量的貢獻率約為![]()
D.若對于變量![]() 與
與![]() 的
的![]() 組統計數據的線性回歸模型中,相關指數
組統計數據的線性回歸模型中,相關指數![]() .又知殘差平方和為
.又知殘差平方和為![]() .那么
.那么![]() .(注意:
.(注意: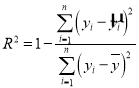 )
)
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,![]() 是正方形ABCD的外接圓,點P在劣弧AB上(P不與A、B重合),DP分別交AO、AB于點Q、T,
是正方形ABCD的外接圓,點P在劣弧AB上(P不與A、B重合),DP分別交AO、AB于點Q、T, ![]() 在點P處的切線交DA的延長線于點E,劣弧BC的中點為F.
在點P處的切線交DA的延長線于點E,劣弧BC的中點為F.

(1)問:何時F、T、E三點共線?請說明理由.
(2)求比值![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某縣共有90間農村淘寶服務站,隨機抽取5間,統計元旦期間的網購金額(單位:萬元)的莖葉圖如圖所示,其中莖為十位數,葉為個位數.若網購金額(單位:萬元)不小于18的服務站定義為優秀服務站,其余為非優秀服務站.從隨機抽取的5間服務站中再任取2間作網購商品的調查,則恰有1間是優秀服務站的概率為_____.
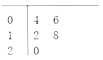
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD﹣A1B1C1D1中,P,Q分別為棱BC和棱CC1的中點,則下列說法正確的是( )
A.BC1//平面AQP
B.平面APQ截正方體所得截面為等腰梯形
C.A1D⊥平面AQP
D.異面直線QP與A1C1所成的角為60°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,以橢圓的2個焦點與1個短軸端點為頂點的三角形的面積為2
,以橢圓的2個焦點與1個短軸端點為頂點的三角形的面積為2![]() 。
。
(1)求橢圓的方程;
(2)如圖,斜率為k的直線l過橢圓的右焦點F,且與橢圓交與A,B兩點,以線段AB為直徑的圓截直線x=1所得的弦的長度為![]() ,求直線l的方程。
,求直線l的方程。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2020年1月10日,引發新冠肺炎疫情的COVID-9病毒基因序列公布后,科學家們便開始了病毒疫苗的研究過程.但是類似這種病毒疫苗的研制需要科學的流程,不是一朝一夕能完成的,其中有一步就是做動物試驗.已知一個科研團隊用小白鼠做接種試驗,檢測接種疫苗后是否出現抗體.試驗設計是:每天接種一次,3天為一個接種周期.已知小白鼠接種后當天出現抗體的概率為![]() ,假設每次接種后當天是否出現抗體與上次接種無關.
,假設每次接種后當天是否出現抗體與上次接種無關.
(1)求一個接種周期內出現抗體次數![]() 的分布列;
的分布列;
(2)已知每天接種一次花費100元,現有以下兩種試驗方案:
①若在一個接種周期內連續2次出現抗體即終止本周期試驗,進行下一接種周期,試驗持續三個接種周期,設此種試驗方式的花費為![]() 元;
元;
②若在一個接種周期內出現2次或3次抗體,該周期結束后終止試驗,已知試驗至多持續三個接種周期,設此種試驗方式的花費為![]() 元.
元.
比較隨機變量![]() 和
和![]() 的數學期望的大小.
的數學期望的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com