
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,焦距為 2,一條準線方程為
,焦距為 2,一條準線方程為![]() ,
,![]() 為橢圓
為橢圓![]() 上一點,直線
上一點,直線![]() 交橢圓
交橢圓![]() 于另一點
于另一點![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 的坐標為
的坐標為![]() ,求過
,求過![]() 三點的圓的方程;
三點的圓的方程;
(3)若![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】分析:(1)根據橢圓的焦距為2,一條準線方程為![]() ,求出a,b,即可求橢圓的方程;
,求出a,b,即可求橢圓的方程;
(2)直線![]() 的方程為x-y+1=0,代入橢圓方程,求出Q的坐標,利用圓的一般方程,建立方程組,即可求過P,Q,
的方程為x-y+1=0,代入橢圓方程,求出Q的坐標,利用圓的一般方程,建立方程組,即可求過P,Q,![]() 三點的圓的方程;
三點的圓的方程;
(3)由![]() ,可得P,Q坐標之間的關系,利用向量數量積公式,結合
,可得P,Q坐標之間的關系,利用向量數量積公式,結合![]() ,利用基本不等式,即可求出
,利用基本不等式,即可求出![]() 的最大值.
的最大值.
解析:解(1)由題意得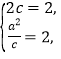 解得
解得![]() ,
,
所以![]() .
.
所以橢圓的方程為![]() .
.
(2)因為![]() ,
,![]() ,所以
,所以![]() 的方程為
的方程為![]() .
.
由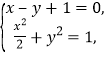 解得
解得![]() 或
或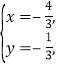
所以點![]() 的坐標為
的坐標為![]() .
.
設過![]() 三點的圓為
三點的圓為![]() ,
,
則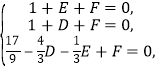 解得
解得![]() .
.
所以圓的方程為![]() .
.
(3)設![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
因為![]() ,所以
,所以![]() 即
即![]()
所以![]() ,
,![]() ,解得
,解得![]() .
.
所以![]()
![]()
![]()
![]()
因為![]() ,所以
,所以![]() ,當且僅當
,當且僅當![]() ,即
,即![]() 時取等號.
時取等號.
所以![]() ,即
,即![]() 的最大值為
的最大值為![]() .
.


科目:高中數學 來源: 題型:
【題目】數列{an}的前n項和為Sn,已知an>0,an2+2an=4Sn+3.
(1)求a1的值;
(2)求{an}的通項公式:
(3)設bn=![]() ,求數列{bn}的前n項和.
,求數列{bn}的前n項和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,橢圓C:
中,橢圓C:![]() 的離心率是
的離心率是![]() ,拋物線E:
,拋物線E:![]() 的焦點F是C的一個頂點.
的焦點F是C的一個頂點.
(Ⅰ)求橢圓C的方程;
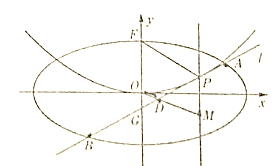
(Ⅱ)設P是E上的動點,且位于第一象限,E在點P處的切線![]() 與C交與不同的兩點A,B,線段AB的中點為D,直線OD與過P且垂直于x軸的直線交于點M.
與C交與不同的兩點A,B,線段AB的中點為D,直線OD與過P且垂直于x軸的直線交于點M.
(i)求證:點M在定直線上;
(ii)直線![]() 與y軸交于點G,記
與y軸交于點G,記![]() 的面積為
的面積為![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的最大值及取得最大值時點P的坐標.
的最大值及取得最大值時點P的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
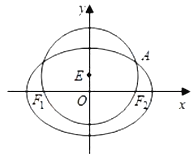
【題目】已知圓![]() :
: ![]() 經過橢圓
經過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() ,且與橢圓
,且與橢圓![]() 在第一象限的交點為
在第一象限的交點為![]() ,且
,且![]() 三點共線,直線
三點共線,直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
, ![]() 兩點,且
兩點,且![]() (
(![]() ).
).
(1)求橢圓![]() 的方程;
的方程;
(2)當三角形![]() 的面積取得最大值時,求直線
的面積取得最大值時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
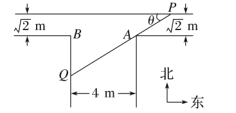
【題目】某“![]() ” 型水渠南北向寬為
” 型水渠南北向寬為![]() ,東西向寬為
,東西向寬為![]() ,其俯視圖如圖所示.假設水渠內的水面始終保持水平位置.
,其俯視圖如圖所示.假設水渠內的水面始終保持水平位置.
(1) 過點![]() 的一條直線與水渠的內壁交于
的一條直線與水渠的內壁交于![]() 兩點,且與水渠的一邊的夾角為
兩點,且與水渠的一邊的夾角為![]() (
(![]() 為銳角),將線段
為銳角),將線段![]() 的長度
的長度![]() 表示為
表示為![]() 的函數;
的函數;
(2) 若從南面漂來一根長度為![]() 的筆直的竹竿(粗細不計),竹竿始終浮于水平面內,且不發生形變,問:這根竹竿能否從拐角處一直漂向東西向的水渠(不會卡住)?試說明理由.
的筆直的竹竿(粗細不計),竹竿始終浮于水平面內,且不發生形變,問:這根竹竿能否從拐角處一直漂向東西向的水渠(不會卡住)?試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 在
在![]() 處取極大值,在
處取極大值,在![]() 處取極小值.
處取極小值.
(1)若![]() ,求函數
,求函數![]() 的單調區間和零點個數;
的單調區間和零點個數;
(2)在方程![]() 的解中,較大的一個記為
的解中,較大的一個記為![]() ;在方程
;在方程![]() 的解中,較小的一個記為
的解中,較小的一個記為![]() ,證明:
,證明:![]() 為定值;
為定值;
(3)證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,取相同的長度單位,若曲線
軸正半軸為極軸建立極坐標系,取相同的長度單位,若曲線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),設
為參數),設![]() 是曲線
是曲線![]() 上任一點,
上任一點,![]() 是曲線
是曲線![]() 上任一點.
上任一點.
(1)求![]() 與
與![]() 交點的極坐標;
交點的極坐標;
(2)已知直線![]() ,點
,點![]() 在曲線
在曲線![]() 上,求點
上,求點![]() 到
到![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】徐州、蘇州兩地相距500千米,一輛貨車從徐州勻速行駛到蘇州,規定速度不得超過100千米/小時.已知貨車每小時的運輸成本(以元為單位)由可變部分和固定部分組成:可變部分與速度v(千米/時)的平方成正比,比例系數為0.01;固定部分為![]() 元(
元(![]() >0).
>0).
(1)把全程運輸成本y(元)表示為速度v(千米/時)的函數,并指出這個函數的定義域;
(2)為了使全程運輸成本最小,汽車應以多大速度行駛?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com