
【題目】設![]() 為數列
為數列![]() 的前n項和,且
的前n項和,且![]() ,當
,當![]() 時,
時,![]() .
.
(I)證明:數列![]() 為等比數列;
為等比數列;
(Ⅱ)記![]() ,求
,求![]() .
.
【答案】(I)見解析(Ⅱ)![]()
【解析】
(I)當n≥2時,(n﹣1)an=(n+1)Sn﹣1+n(n﹣1),n∈N*.可得(n﹣1)(Sn﹣Sn﹣1)=(n+1)Sn﹣1+n(n﹣1),化為:![]() 1=2(
1=2(![]() 1),
1),![]() 1=2.即可證明.
1=2.即可證明.
(II)由(I)可得:![]() 1=2n,可得:Sn=n2n﹣n.設數列{n2n}的前n項和為An.利用錯位相減法即可得出An,再寫出
1=2n,可得:Sn=n2n﹣n.設數列{n2n}的前n項和為An.利用錯位相減法即可得出An,再寫出![]() 即可.
即可.
(I)當![]() 時,
時,![]() ,
,
所以![]() ,
,
即![]() ,則
,則![]() ,
,
所以![]() ,又
,又![]() ,
,
故數列![]() 是首項為2,公比為2的等比數列.
是首項為2,公比為2的等比數列.
(II)由(I)可得:![]() 1=2n,可得:Sn=n2n﹣n.
1=2n,可得:Sn=n2n﹣n.
設數列{n2n}的前n項和為An.
∴An=2+222+323+……+n2n,
2An=22+223+……+(n﹣1)2n+n2n+1,
∴﹣An=2+22+……+2n﹣n2n+1![]() n2n+1,
n2n+1,
可得:An=(n﹣1)2n+1+2.
∴Tn=S1+S2+…+Sn=(n﹣1)2n+1+2![]() .
.


科目:高中數學 來源: 題型:
【題目】[2019·清遠期末]一只紅鈴蟲的產卵數![]() 和溫度
和溫度![]() 有關,現收集了4組觀測數據列于下表中,根據數據作出散點圖如下:
有關,現收集了4組觀測數據列于下表中,根據數據作出散點圖如下:
溫度 | 20 | 25 | 30 | 35 |
產卵數 | 5 | 20 | 100 | 325 |

(1)根據散點圖判斷![]() 與
與![]() 哪一個更適宜作為產卵數
哪一個更適宜作為產卵數![]() 關于溫度
關于溫度![]() 的回歸方程類型?(給出判斷即可,不必說明理由)
的回歸方程類型?(給出判斷即可,不必說明理由)
(2)根據(1)的判斷結果及表中數據,建立![]() 關于
關于![]() 的回歸方程(數字保留2位小數);
的回歸方程(數字保留2位小數);
(3)要使得產卵數不超過50,則溫度控制在多少![]() 以下?(最后結果保留到整數)
以下?(最后結果保留到整數)
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
| 5 | 20 | 100 | 325 |
| 1.61 | 3 | 4.61 | 5.78 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面是邊長為
的底面是邊長為![]() 的菱形,
的菱形,![]() ,點
,點![]() 是棱
是棱![]() 的中點,
的中點,![]() ,點
,點![]() 在平面
在平面![]() 的射影為
的射影為![]() ,
,![]() 為棱
為棱![]() 上一點,
上一點,
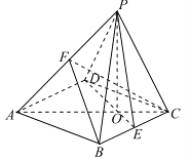
(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 為棱
為棱![]() 的中點,
的中點,![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ax+b,g(x)=ex(cx+d),若曲線y=f(x)和曲線y=g(x)都過點P(0,2),且在點P處有相同的切線y=4x+2.
(1)求a,b,c,d的值;
(2)若x≥-2時,恒有f(x)≤kg(x),求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,正四棱椎P-ABCD中,底面ABCD的邊長為2,側棱長為![]() .
.

(I)若點E為PD上的點,且PB∥平面EAC.試確定E點的位置;
(Ⅱ)在(I)的條件下,點F為線段PA上的一點且![]() ,若平面AEC和平面BDF所成的銳二面角的余弦值為
,若平面AEC和平面BDF所成的銳二面角的余弦值為![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在四棱錐P-ABCD中,底面ABCD是邊長為2的菱形,側面![]() 底面ABCD,
底面ABCD,![]() ,
,![]() ,E,Q分別是BC和PC的中點.
,E,Q分別是BC和PC的中點.
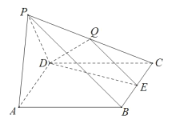
(I)求直線BQ與平面PAB所成角的正弦值;
(Ⅱ)求二面角E-DQ-P的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間![]() ,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
,需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
![]()
以最高氣溫位于各區間的頻率代替最高氣溫位于該區間的概率.
(1)求六月份這種酸奶一天的需求量![]() (單位:瓶)的分布列;
(單位:瓶)的分布列;
(2)設六月份一天銷售這種酸奶的利潤為![]() (單位:元),當六月份這種酸奶一天的進貨量
(單位:元),當六月份這種酸奶一天的進貨量![]() (單位:瓶)為多少時?
(單位:瓶)為多少時?![]() 的數學期望達到最大值?
的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2011年,國際數學協會正式宣布,將每年的3月14日設為“國際數學節”,其來源是中國古代數學家祖沖之的圓周率,為慶祝該節日,某校舉辦的“數學嘉年華”活動中,設計了如下的有獎闖關游戲:參賽選手按第一關、第二關、第三關的順序依次闖關,若闖關成功,則分別獲得5個、10個、20個學豆的獎勵.游戲還規定:當選手闖過一關后,可以選擇帶走相應的學豆,結束游戲;也可以選擇繼續闖下一關,若有任何一關沒有闖關成功,則全部學豆歸零,游戲結束.設選手甲能闖過第一關、第二關、第三關的概率分別為![]() ,選手選擇繼續闖關的概率均為
,選手選擇繼續闖關的概率均為![]() ,且各關之間闖關成功與否互不影響.
,且各關之間闖關成功與否互不影響.
(1)求選手甲第一關闖關成功且所得學豆為零的概率;
(2)設該選手所得學豆總數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com