
【題目】如圖,已知矩形![]() ,過
,過![]() 作
作![]() 平面
平面![]() ,再過
,再過![]() 作
作![]() 于點
于點![]() ,過
,過![]() 作
作![]() 于點
于點![]() .
.
(Ⅰ)求證: ![]() .
.
(Ⅱ)若平面![]() 交
交![]() 于點
于點![]() ,求證:
,求證: ![]() .
.
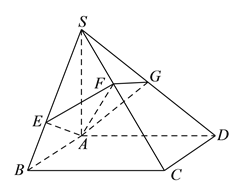
【答案】(1)見解析(2)見解析
【解析】試題分析:(1)本題需經過多次線面垂直與線線垂直的轉化:由![]() 平面
平面![]() ,得
,得![]() ,再得
,再得![]() 平面
平面![]() ,即得
,即得![]() ,可得
,可得![]() 平面
平面![]() ,即得
,即得![]() ,因此
,因此![]() 平面
平面![]() ,即得結論(2)本題仍需經過多次線面垂直與線線垂直的轉化:由
,即得結論(2)本題仍需經過多次線面垂直與線線垂直的轉化:由![]() 平面
平面![]() ,得
,得![]() ,再得
,再得![]() 平面
平面![]() ,即得
,即得![]() ,可得
,可得![]() 平面
平面![]() ,即得結論
,即得結論
試題解析:(Ⅰ)∵在矩形![]() 中,
中,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 點,
點,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,
![]() 點,
點,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() ,
,
![]() 點,
點,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)∵在矩形![]() 中,
中,
∴![]() ,
,
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 點,
點,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 點,
點,
![]() 、
、![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .
.
點睛:垂直、平行關系證明中應用轉化與化歸思想的常見類型.
(1)證明線面、面面平行,需轉化為證明線線平行.
(2)證明線面垂直,需轉化為證明線線垂直.
(3)證明線線垂直,需轉化為證明線面垂直.


科目:高中數學 來源: 題型:
【題目】已知⊙![]() :
: ![]() 與⊙
與⊙![]() :
: ![]() ,以
,以![]() ,
, ![]() 分別為左右焦點的橢圓
分別為左右焦點的橢圓![]() :
: ![]() 經過兩圓的交點。
經過兩圓的交點。
(Ⅰ)求橢圓![]() 的方程;
的方程;
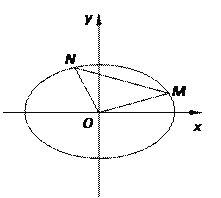
(Ⅱ)![]() 、
、![]() 是橢圓
是橢圓![]() 上的兩點,若直線
上的兩點,若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,試問
,試問![]() 的面積是否為定值?若是,求出這個定值;若不是,請說明理由。
的面積是否為定值?若是,求出這個定值;若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知冪函數f(x)=(﹣2m2+m+2)xm+1為偶函數.
(1)求f(x)的解析式;
(2)若函數y=f(x)﹣2(a﹣1)x+1在區間(2,3)上為單調函數,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的偶函數,當x≥0時,f(x)=x2﹣2x﹣1.
(1)求f(x)的函數解析式;
(2)作出函數f(x)的簡圖,寫出函數f(x)的單調減區間及最值.
(3)若關于x的方程f(x)=m有兩個解,試說出實數m的取值范圍.(只要寫出結果,不用給出證明過程)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為了解廣告投入對銷售收益的影響,在若干地區各投入![]() 萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從
萬元廣告費用,并將各地的銷售收益繪制成頻率分布直方圖(如圖所示).由于工作人員操作失誤,橫軸的數據丟失,但可以確定橫軸是從![]() 開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
開始計數的. [附:回歸直線的斜率和截距的最小二乘估計公式分別為.]
(1)根據頻率分布直方圖計算圖中各小長方形的寬度;
(2)試估計該公司投入![]() 萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
萬元廣告費用之后,對應銷售收益的平均值(以各組的區間中點值代表該組的取值);
(3)該公司按照類似的研究方法,測得另外一些數據,并整理得到下表:
廣告投入 | 1 | 2 | 3 | 4 | 5 |
銷售收益 | 2 | 3 | 2 | 7 |
由表中的數據顯示, ![]() 與
與![]() 之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出
之間存在著線性相關關系,請將(2)的結果填入空白欄,并求出![]() 關于
關于![]() 的回歸直線方程.
的回歸直線方程.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() ,向量
,向量 ![]() ,函數f(x)=
,函數f(x)= ![]() .
.
(1)求函數f(x)的單調遞增區間;
(2)將函數y=f(x)的圖象上所有點向右平行移動 ![]() 個單位長度,得函數y=g(x)的圖象,求函數y=g(x)在區間[0,π]上的值域.
個單位長度,得函數y=g(x)的圖象,求函數y=g(x)在區間[0,π]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某市為了引導居民合理用水,居民生活用水實行二級階梯式水價計量辦法,具體如下:第一階梯,每戶居民月用水量不超過12噸,價格為4元/噸;第二階梯,每戶居民月用水量超過12噸,超過部分的價格為8元/噸.為了了解全市居民月用水量的分布情況,通過抽樣獲得了100戶居民的月用水量(單位:噸),將數據按照![]() ,
, ![]() ,…,
,…, ![]() 分成8組,制成了如圖1所示的頻率分布直方圖.
分成8組,制成了如圖1所示的頻率分布直方圖.

(圖1) (圖2)
(Ⅰ)求頻率分布直方圖中字母![]() 的值,并求該組的頻率;
的值,并求該組的頻率;
(Ⅱ)通過頻率分布直方圖,估計該市居民每月的用水量的中位數![]() 的值(保留兩位小數);
的值(保留兩位小數);
(Ⅲ)如圖2是該市居民張某2016年1~6月份的月用水費![]() (元)與月份
(元)與月份![]() 的散點圖,其擬合的線性回歸方程是
的散點圖,其擬合的線性回歸方程是![]() . 若張某2016年1~7月份水費總支出為312元,試估計張某7月份的用水噸數.
. 若張某2016年1~7月份水費總支出為312元,試估計張某7月份的用水噸數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com