
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 為矩形,平面
為矩形,平面![]() 平面
平面![]() ,
,![]() 為
為![]() 中點,
中點,![]() .
.

(1)求證:![]() ;
;
(2)若![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,求二面角
,求二面角![]() 的大小.
的大小.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)由面面垂直的性質定理可得出![]() 平面
平面![]() ,可得出
,可得出![]() ,由等腰三角形三線合一的性質可得出
,由等腰三角形三線合一的性質可得出![]() ,由此可得出
,由此可得出![]() 平面
平面![]() ,進而得出
,進而得出![]() ;
;
(2)設![]() ,可得出
,可得出![]() ,
,![]() ,由(1)可知,
,由(1)可知,![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,可得
,可得![]() ,進而以點
,進而以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 、
、![]() 、
、![]() 軸建立空間直角坐標系,利用空間向量法可求出二面角
軸建立空間直角坐標系,利用空間向量法可求出二面角![]() 的大小.
的大小.
(1)![]() 四邊形
四邊形![]() 為矩形,則
為矩形,則![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 面
面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
又![]() ,
,![]() 為
為![]() 中點,
中點,![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,故
,故![]() ;
;
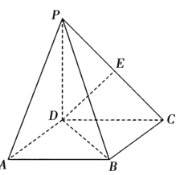
(2)不妨設![]() ,由
,由![]() 得
得![]() ,由(1)得
,由(1)得![]() ,∴
,∴![]() ,∴
,∴![]() ,由(1)得
,由(1)得![]() 平面
平面![]() ,
,
由(1)知,![]() 在平面
在平面![]() 的射影為
的射影為![]() ,即
,即![]() ,
,
![]() ,故
,故![]() .
.
以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 、
、![]() 、
、![]() 軸建立如下圖所示的空間直角坐標系
軸建立如下圖所示的空間直角坐標系![]() ,
,
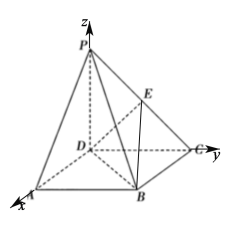
易得![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
設平面![]() 與平面
與平面![]() 的法向量分別為
的法向量分別為![]() 和
和![]() ,
,
則![]() ,
,
由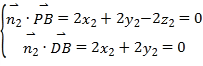 ,令
,令![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
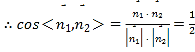 ,設二面角
,設二面角![]() 的大小為
的大小為![]() ,則
,則![]() ,所以二面角
,所以二面角![]() 的大小
的大小![]()


 新思維假期作業(yè)寒假吉林大學出版社系列答案
新思維假期作業(yè)寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】2016年1月14日,國防科工局宣布,嫦娥四號任務已經通過了探月工程重大專項領導小組審議通過,正式開始實施.如圖所示,假設“嫦娥四號”衛(wèi)星將沿地月轉移軌道飛向月球后,在月球附近一點P變軌進入以月球球心F為一個焦點的橢圓軌道Ⅰ繞月飛行,之后衛(wèi)星在P點第二次變軌進入仍以F為一個焦點的橢圓軌道Ⅱ繞月飛行.若用![]() 和
和![]() 分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用
分別表示橢圓軌道Ⅰ和Ⅱ的焦距,用![]() 和
和![]() 分別表示橢圓軌道Ⅰ和Ⅱ的長軸長,給出下列式子:①
分別表示橢圓軌道Ⅰ和Ⅱ的長軸長,給出下列式子:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確式子的序號是( )
.其中正確式子的序號是( )

A.①③B.①④C.②③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在水平地面上的不同兩點處栽有兩根筆直的電線桿,假設它們都垂直于地面,則在水平地面上視它們上端仰角相等的點![]() 的軌跡可能是( )
的軌跡可能是( )
①直線 ②圓 ③橢圓 ④拋物線
A.①②B.①③C.①②③D.②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求![]() 與
與![]() 的交點的直角坐標;
的交點的直角坐標;
(2)求![]() 上的點到直線
上的點到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() 的左、右頂點分別為
的左、右頂點分別為![]() ,上、下頂點分別為
,上、下頂點分別為![]() ,左、右焦點分別為
,左、右焦點分別為![]() ,
,![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過右焦點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,試探究在
兩點,試探究在![]() 軸上是否存在定點
軸上是否存在定點![]() ,使得可
,使得可![]() 為定值?若存在,求出點
為定值?若存在,求出點![]() 的坐標,若不存在,請說明理由?
的坐標,若不存在,請說明理由?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知平行于
中,已知平行于![]() 軸的動直線
軸的動直線![]() 交拋物線
交拋物線![]() :
: ![]() 于點
于點![]() ,點
,點![]() 為
為![]() 的焦點.圓心不在
的焦點.圓心不在![]() 軸上的圓
軸上的圓![]() 與直線
與直線![]() ,
, ![]() ,
, ![]() 軸都相切,設
軸都相切,設![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求曲線![]() 的方程;
的方程;
(2)若直線![]() 與曲線
與曲線![]() 相切于點
相切于點![]() ,過
,過![]() 且垂直于
且垂直于![]() 的直線為
的直線為![]() ,直線
,直線![]() ,
, ![]() 分別與
分別與![]() 軸相交于點
軸相交于點![]() ,
, ![]() .當線段
.當線段![]() 的長度最小時,求
的長度最小時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(x>0).
,(x>0).
(1)當0<a<b,且f(a)=f(b)時,求證:ab>1;
(2)是否存在實數a,b(a<b),使得函數y=f(x)的定義域、值域都是[a,b],若存在,則求出a,b的值,若不存在,請說明理由.
(3)若存在實數a,b(a<b),使得函數y=f(x)的定義域為[a,b]時,值域為[ma,mb](m≠0),求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數學老師給出一個函數![]() ,甲、乙、丙、丁四個同學各說出了這個函數的一條性質:甲:在
,甲、乙、丙、丁四個同學各說出了這個函數的一條性質:甲:在![]() 上函數單調遞減;乙:在
上函數單調遞減;乙:在![]() 上函數單調遞增;丙:在定義域R上函數的圖象關于直線
上函數單調遞增;丙:在定義域R上函數的圖象關于直線![]() 對稱;丁:
對稱;丁:![]() 不是函數的最小值.老師說:你們四個同學中恰好有三個人說的正確.那么,你認為____說的是錯誤的.
不是函數的最小值.老師說:你們四個同學中恰好有三個人說的正確.那么,你認為____說的是錯誤的.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校將甲、乙等6名新招聘的老師分配到4個不同的年級,每個年級至少分配1名教師,且甲、乙兩名老師必須分到同一個年級,則不同的分法種數為______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com