
【題目】已知數(shù)列{an}的前![]() 項(xiàng)和為
項(xiàng)和為![]() ,數(shù)列{bn},{cn}滿足
,數(shù)列{bn},{cn}滿足![]() ,
, ![]() ,其中
,其中![]() .
.
(1)若數(shù)列{an}是公差為2的等差數(shù)列,求數(shù)列{cn}的通項(xiàng)公式;
(2)若存在實(shí)數(shù)λ,使得對(duì)一切![]() ,有bn≤λ≤cn,求證:數(shù)列{an}是等差數(shù)列.
,有bn≤λ≤cn,求證:數(shù)列{an}是等差數(shù)列.
【答案】(1)cn=1.(2)見解析.
【解析】試題分析:(1)由題意得,根據(jù)等差數(shù)列的通項(xiàng)公式求得![]() ,即可
,即可![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)由![]() ,遞推化簡(jiǎn),得到
,遞推化簡(jiǎn),得到![]() ,因?yàn)橐磺?/span>
,因?yàn)橐磺?/span>![]() ,都有
,都有![]() ,得到
,得到![]() ,得到
,得到![]() ,再利用等差數(shù)列的性質(zhì),即可得到數(shù)列
,再利用等差數(shù)列的性質(zhì),即可得到數(shù)列![]() 為等差數(shù)列。
為等差數(shù)列。
試題解析: (1)因?yàn)閧an}是公差為2的等差數(shù)列,
所以an=a1+2(n-1),![]() =a1+n-1,從而 (n+2)
=a1+n-1,從而 (n+2)
cn=![]() -(a1+n-1)=n+2,即cn=1.
-(a1+n-1)=n+2,即cn=1.
(2)由(n+1)bn=an+1-![]() ,
,
得n(n+1) bn=nan+1-Sn,
(n+1)(n+2) bn+1=(n+1)an+2-Sn+1,
兩式相減,并化簡(jiǎn)得an+2-an+1=(n+2) bn+1-nbn.
從而 (n+2) cn=![]() -
-![]() =
=![]() -[an+1-(n+1) bn]
-[an+1-(n+1) bn]
=![]() +(n+1) bn
+(n+1) bn
=![]() +(n+1) bn
+(n+1) bn
= (n+2)( bn+bn+1).
因此cn= ( bn+bn+1).
因?yàn)閷?duì)一切n∈N*,有bn≤λ≤cn,所以λ≤cn= (bn+bn+1)≤λ,
故bn=λ,cn=λ.
所以 (n+1)λ=an+1-![]() , ①
, ①
(n+2)λ= (an+1+an+2)-![]() , ②
, ②
②-①,得 (an+2-an+1)=λ,即an+2-an+1=2λ.
故an+1-an=2λ (n≥2).
又2λ=a2-![]() =a2-a1,則an+1-an=2λ (n≥1).
=a2-a1,則an+1-an=2λ (n≥1).
所以數(shù)列{an}是等差數(shù)列.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)= ![]() -
-![]() ,g(x)=
,g(x)= ![]() .
.
(1)若![]() ,函數(shù)
,函數(shù)![]() 的圖像與函數(shù)
的圖像與函數(shù)![]() 的圖像相切,求
的圖像相切,求![]() 的值;
的值;
(2)若![]() ,
, ![]() ,函數(shù)
,函數(shù)![]() 滿足對(duì)任意
滿足對(duì)任意![]() (x1
(x1![]() x2),都有
x2),都有![]() 恒成立,求
恒成立,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,函數(shù)
,函數(shù)![]() =f(x)+ g(x),且G(
=f(x)+ g(x),且G(![]() )有兩個(gè)極值點(diǎn)x1,x2,其中x1
)有兩個(gè)極值點(diǎn)x1,x2,其中x1![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列![]() 中,
中, ![]() ,前
,前![]() 項(xiàng)和
項(xiàng)和![]() 滿足
滿足![]() (
(![]() ).
).
⑴ 求數(shù)列![]() 的通項(xiàng)公式;
的通項(xiàng)公式;
⑵ 記![]() ,求數(shù)列
,求數(shù)列![]() 的前
的前![]() 項(xiàng)和
項(xiàng)和![]() ;
;
⑶ 是否存在整數(shù)對(duì)![]() (其中
(其中![]() ,
, ![]() )滿足
)滿足![]() ?若存在,求出所有的滿足題意的整數(shù)對(duì)
?若存在,求出所有的滿足題意的整數(shù)對(duì)![]() ;若不存在,請(qǐng)說明理由.
;若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的圖象在
的圖象在![]() 處的切線方程;
處的切線方程;
(2)若函數(shù)![]() 在定義域上為單調(diào)增函數(shù).
在定義域上為單調(diào)增函數(shù).
①求![]() 最大整數(shù)值;
最大整數(shù)值;
②證明: ![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱臺(tái)![]() 中, 側(cè)面
中, 側(cè)面![]() 與側(cè)面
與側(cè)面![]() 是全等的梯形,若
是全等的梯形,若![]() ,且
,且![]() .
.

(Ⅰ)若![]() ,
, ![]() ,證明:
,證明: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)若二面角![]() 為
為![]() ,求平面
,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】隨著資本市場(chǎng)的強(qiáng)勢(shì)進(jìn)入,互聯(lián)網(wǎng)共享單車“忽如一夜春風(fēng)來”,遍布了一二線城市的大街小巷.為了解共享單車在![]() 市的使用情況,某調(diào)查機(jī)構(gòu)借助網(wǎng)絡(luò)進(jìn)行了問卷調(diào)查,并從參與調(diào)查的網(wǎng)友中抽取了200人進(jìn)行抽樣分析,得到表格:(單位:人)
市的使用情況,某調(diào)查機(jī)構(gòu)借助網(wǎng)絡(luò)進(jìn)行了問卷調(diào)查,并從參與調(diào)查的網(wǎng)友中抽取了200人進(jìn)行抽樣分析,得到表格:(單位:人)
經(jīng)常使用 | 偶爾或不用 | 合計(jì) | |
30歲及以下 | 70 | 30 | 100 |
30歲以上 | 60 | 40 | 100 |
合計(jì) | 130 | 70 | 200 |
(1)根據(jù)以上數(shù)據(jù),能否在犯錯(cuò)誤的概率不超過0.15的前提下認(rèn)為![]() 市使用共享單車情況與年齡有關(guān)?
市使用共享單車情況與年齡有關(guān)?
(2)現(xiàn)從所抽取的30歲以上的網(wǎng)友中利用分層抽樣的方法再抽取5人.從這5人中,再隨機(jī)選出2人贈(zèng)送一件禮品,求選出的2人中至少有1人經(jīng)常使用共享單車的概率.
參考公式: 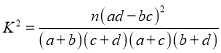 ,其中
,其中![]() .
.
參考數(shù)據(jù):
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點(diǎn),
的中點(diǎn),![]() 是等腰三角形,
是等腰三角形,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 上一點(diǎn).
上一點(diǎn).
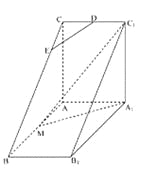
(I)若![]() 平面
平面![]() ,求
,求![]() ;
;
(II)平面![]() 將三棱柱
將三棱柱![]() 分成兩個(gè)部分,求較小部分與較大部分的體積之比.
分成兩個(gè)部分,求較小部分與較大部分的體積之比.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com