
(本小題滿分10分)已知集合A={x|x2-3x+2=0},B={x|x2-ax+3a-5=0}.若A∩B=B,求實數a的取值范圍.
當2≤a<10時,均有A∩B=B.
【解析】主要考查集合的子集、交集運算。首先得出A={1,2},在由A∩B=B得出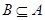 ,從而根據B=
,從而根據B=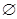 及B≠
及B≠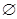 兩種情況,討論x2-ax+3a-5=0根的判別式Δ<0, Δ≥0時a的取值。
兩種情況,討論x2-ax+3a-5=0根的判別式Δ<0, Δ≥0時a的取值。
解:A={x|x2-3x+2=0}={1,2},
由x2-ax+3a-5=0,知Δ=a2-4(3a-5)=a2-12a+20=(a-2)(a-10).
(1)當2<a<10時,Δ<0,B=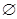
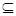 A;
A;
(2)當a≤2或a≥10時,Δ≥0,則B≠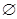 .
.
若x=1,則1-a+3a-5=0,得a=2,
此時B={x|x2-2x+1=0}={1}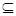 A;
A;
若x=2,則4-2a+3a-5=0,得a=1,
此時B={2,-1}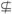 A.
A.
綜上所述,當2≤a<10時,均有A∩B=B.


科目:高中數學 來源: 題型:
 (選做題)本題包括A、B、C、D四小題,請選定其中兩題,并在答題卡指定區域內作答,若多做,則按作答的前兩題評分,解答時應寫出文字說明、證明過程或演算步驟.
(選做題)本題包括A、B、C、D四小題,請選定其中兩題,并在答題卡指定區域內作答,若多做,則按作答的前兩題評分,解答時應寫出文字說明、證明過程或演算步驟.
|
|
| 1 |
| 2a |
| 1 |
| 2b |
| 1 |
| 2c |
| 1 |
| b+c |
| 1 |
| c+a |
| 1 |
| a+b |
查看答案和解析>>
科目:高中數學 來源: 題型:
 本題包括(1)、(2)、(3)、(4)四小題,請選定其中兩題,并在答題卡指定區域內答,
本題包括(1)、(2)、(3)、(4)四小題,請選定其中兩題,并在答題卡指定區域內答,
|
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com