
【題目】已知橢圓C的對稱中心為坐標原點O,焦點在x軸上,左右焦點分別為F,F,左右頂點分別為A,B,且|F1F2|=4,|AB|=4 ![]()
(1)求橢圓的方程;
(2)過F1的直線l與橢圓C相交于M,N兩點,若△MF2N的面積為 ![]() ,求直線l的方程.
,求直線l的方程.
【答案】
(1)解:∵橢圓C的對稱中心為坐標原點O,焦點在x軸上,
左右焦點分別為F,F,左右頂點分別為A,B,且|F1F2|=4,|AB|=4 ![]() ,
,
∴ 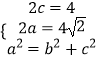 ,解得a=2
,解得a=2 ![]() ,c=2,b=2,
,c=2,b=2,
∴橢圓的方程為 ![]()
(2)解:由(1)知F1(﹣2,0),設過F1的直線l的方程為:x+2=my,
由 ![]() ,得(m2+2)y2﹣4my﹣4=0,
,得(m2+2)y2﹣4my﹣4=0,
設M(x1,y1),N(x2,y2),則 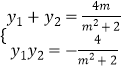 ,
,
∵△MF2N的面積為 ![]() ,
,
∴ ![]() =
= ![]() =2
=2 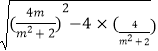 =
= ![]() ,
,
化簡,得2m4﹣m2﹣1=0,解得m2=1或m2=﹣ ![]() (舍),
(舍),
解得m=±1,此時直線l的方程為x﹣y+2=0,或x+y+2=0
【解析】(1)由|F1F2|=4,|AB|=4 ![]() ,建立方程組,求出a=2
,建立方程組,求出a=2 ![]() ,c=2,b=2,由此能求出橢圓的方程.(2)由F1(﹣2,0),設過F1的直線l的方程為:x+2=my,由
,c=2,b=2,由此能求出橢圓的方程.(2)由F1(﹣2,0),設過F1的直線l的方程為:x+2=my,由 ![]() ,得(m2+2)y2﹣4my﹣4=0,利用韋達定理、弦長公式、三角形面積公式,能求出m=±1,由此能求出直線l的方程.
,得(m2+2)y2﹣4my﹣4=0,利用韋達定理、弦長公式、三角形面積公式,能求出m=±1,由此能求出直線l的方程.


科目:高中數學 來源: 題型:
【題目】某創業投資公司擬開發某種新能源產品,估計能獲得![]() 萬元到
萬元到![]() 萬元的投資利益,現準備制定一個對科研課題組的獎勵方案:獎金
萬元的投資利益,現準備制定一個對科研課題組的獎勵方案:獎金![]() (單位:萬元)隨投資收益
(單位:萬元)隨投資收益![]() (單位:萬元)的增加而增加,且獎金不超過
(單位:萬元)的增加而增加,且獎金不超過![]() 萬元,同時獎金不超過收益的
萬元,同時獎金不超過收益的![]() .
.
(![]() )請分析函數
)請分析函數![]() 是否符合公司要求的獎勵函數模型,并說明原因.
是否符合公司要求的獎勵函數模型,并說明原因.
(![]() )若該公司采用函數模型
)若該公司采用函數模型![]() 作為獎勵函數模型,試確定最小正整數
作為獎勵函數模型,試確定最小正整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據IEC(國際電工委員會)調查顯示,小型風力發電項目投資較少,且開發前景廣闊,但受風力自然資源影響,項目投資存在一定風險.根據測算,風能風區分類標準如下:
風能分類 | 一類風區 | 二類風區 |
平均風速m/s | 8.5~10 | 6.5~8.5 |
假設投資A項目的資金為x(x≥0)萬元,投資B項目資金為y(y≥0)萬元,調研結果是:未來一年內,位于一類風區的A項目獲利30%的可能性為0.6,虧損20%的可能性為0.4;位于二類風區的B項目獲利35%的可能性為0.6,虧損10%的可能性是0.1,不賠不賺的可能性是0.3.
(1)記投資A,B項目的利潤分別為ξ和η,試寫出隨機變量ξ與η的分布列和期望Eξ,Eη;
(2)某公司計劃用不超過100萬元的資金投資于A,B項目,且公司要求對A項目的投資不得低于B項目,根據(1)的條件和市場調研,試估計一年后兩個項目的平均利潤之和z=Eξ+Eη的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】四邊形OABC的四個頂點坐標分別為O(0,0)、A(6,2)、B(4,6)、C(2,6),直線y=kx(![]() <k<3)分四邊形OABC為兩部分,S表示靠近x軸一側的那一部分的面積.
<k<3)分四邊形OABC為兩部分,S表示靠近x軸一側的那一部分的面積.
(1)求S=f(k)的函數表達式;
(2)當k為何值時,直線y=kx將四邊形OABC分為面積相等的兩部分?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:Sn=1﹣an(n∈N*),其中Sn為數列{an}的前n項和. (Ⅰ)試求{an}的通項公式;
(Ⅱ)若數列{bn}滿足: ![]() (n∈N*),試求{bn}的前n項和公式Tn .
(n∈N*),試求{bn}的前n項和公式Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,直線l的參數方程為  (t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為3ρ2cos2θ+4ρ2sin2θ=12.
(t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為3ρ2cos2θ+4ρ2sin2θ=12.
(Ⅰ)求曲線C的直角坐標方程;
(Ⅱ)已知直線l與曲線C交于A,B兩點,試求|AB|.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義:若函數![]() 的定義域為
的定義域為![]() ,且存在非零常數
,且存在非零常數![]() ,對任意
,對任意![]()
![]() ,
, ![]() 恒成立,則稱
恒成立,則稱![]() 為線周期函數,
為線周期函數, ![]() 為
為![]() 的線周期.
的線周期.
(1)下列函數①![]() ,②
,②![]() ,③
,③![]() (其中
(其中![]() 表示不超過x的最大整數),是線周期函數的是 (直接填寫序號);
表示不超過x的最大整數),是線周期函數的是 (直接填寫序號);
(2)若![]() 為線周期函數,其線周期為
為線周期函數,其線周期為![]() ,求證:
,求證: ![]() 為周期函數;
為周期函數;
(3)若![]() 為線周期函數,求
為線周期函數,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com