Question

（07年湖南卷理）（12分）

已知雙曲線的左、右焦點分別為，，過點的動直線與雙曲線相交于兩點．

（I）若動點滿足（其中為坐標原點），求點的軌跡方程；

（II）在軸上是否存在定點，使?為常數？若存在，求出點的坐標；

若不存在，請說明理由．

Answer 1

解析：由條件知，，設，．

解法一：（I）設，則則，，

，由得

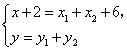即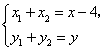

于是的中點坐標為．

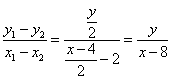當不與軸垂直時，，即．

又因為兩點在雙曲線上，所以，，兩式相減得

，即．

將代入上式，化簡得．

當與軸垂直時，，求得，也滿足上述方程．

所以點的軌跡方程是．

（II）假設在軸上存在定點，使為常數．

當不與軸垂直時，設直線的方程是．

代入有．

則是上述方程的兩個實根，所以，，

于是

．

因為是與無關的常數，所以，即，此時=．

當與軸垂直時，點的坐標可分別設為，，

此時．

故在軸上存在定點，使為常數．

解法二：（I）同解法一的（I）有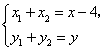

當不與軸垂直時，設直線的方程是．

代入有．

則是上述方程的兩個實根，所以．

．

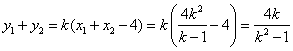由①②③得．…………………………………………………④

．……………………………………………………………………⑤

當時，，由④⑤得，，將其代入⑤有

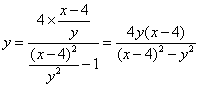．整理得．

當時，點的坐標為，滿足上述方程．

當與軸垂直時，，求得，也滿足上述方程．

故點的軌跡方程是．

（II）假設在軸上存在定點點，使為常數，

當不與軸垂直時，由（I）有，．

以上同解法一的（II）．