
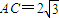 ,點B是橢圓
,點B是橢圓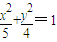 的上頂點,l是雙曲線x2-y2=-2位于x軸下方的準線,當AC在直線l上運動時.
的上頂點,l是雙曲線x2-y2=-2位于x軸下方的準線,當AC在直線l上運動時. )作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.
)作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.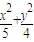 =1及雙曲線方程x2-y2=-2可得點B(0,2),直線l的方程是y=-1.
=1及雙曲線方程x2-y2=-2可得點B(0,2),直線l的方程是y=-1.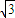 ,且AC在直線l上運動.
,且AC在直線l上運動.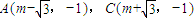 ,則AC的垂直平分線方程為x=m①
,則AC的垂直平分線方程為x=m①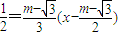 ②
②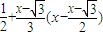 ,即y=
,即y=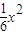 .
.
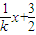
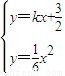 得x2-6kx-9=0∵△=36k2+36>0,∴直線l1與軌跡E交于兩點.
得x2-6kx-9=0∵△=36k2+36>0,∴直線l1與軌跡E交于兩點.
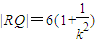
 |MN|•|QF|+
|MN|•|QF|+ |MN|•|RF|=
|MN|•|RF|= |MN|(|QF|+|RF|)=
|MN|(|QF|+|RF|)=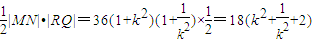 ≥
≥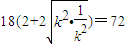
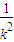 ,即k=±1時,等號成立.故四邊形MRNQ的面積的最小值為72.
,即k=±1時,等號成立.故四邊形MRNQ的面積的最小值為72.

 名師金手指領銜課時系列答案
名師金手指領銜課時系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
(本大題滿分13分)
在△ABC中,![]() ,點B是橢圓
,點B是橢圓![]() 的上頂點,l是雙曲線
的上頂點,l是雙曲線![]() 位于x軸下方的準線,當AC在直線l上運動時.
位于x軸下方的準線,當AC在直線l上運動時.
(1)求△ABC外接圓的圓心![]() 的軌跡E的方程;
的軌跡E的方程;
(2)過定點F(0,![]() )作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.
)作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
20.(本大題滿分13分)
在△ABC中,![]() ,點B是橢圓
,點B是橢圓![]() 的上頂點,l是雙曲線
的上頂點,l是雙曲線![]() 位于x軸下方的準線,當AC在直線l上運動時.
位于x軸下方的準線,當AC在直線l上運動時.
(1)求△ABC外接圓的圓心![]() 的軌跡E的方程;
的軌跡E的方程;
(2)過定點F(0,![]() )作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.
)作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.
查看答案和解析>>
科目:高中數學 來源:2008-2009學年湖北省黃岡中學高三(下)2月月考數學試卷(理科)(解析版) 題型:解答題
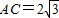 ,點B是橢圓
,點B是橢圓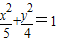 的上頂點,l是雙曲線x2-y2=-2位于x軸下方的準線,當AC在直線l上運動時.
的上頂點,l是雙曲線x2-y2=-2位于x軸下方的準線,當AC在直線l上運動時. )作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.
)作互相垂直的直線l1、l2,分別交軌跡E于點M、N和點R、Q.求四邊形MRNQ的面積的最小值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com