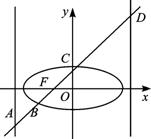
構建問題:如圖,已知橢圓 =1(2≤m≤5),過其左焦點且斜率為1的直線與橢
=1(2≤m≤5),過其左焦點且斜率為1的直線與橢
圓及其準線的交點從左到右的順序為A、B、C、D.設f(m)=||AB|-|CD||,試求f(m)的解析式.
解析:(1)設橢圓的長半軸、短半軸及半焦距依次為a、b、c,則a2=m,b2=m-1,c2=a2-b2=1,∴橢圓的焦點為F1(-1,0),F2(1,0).故直線的方程為y=x+1.又橢圓的準線方程為x=±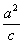 ,即x=±m,∴A(-m,-m+1),D(m,m+1).考慮方程組
,即x=±m,∴A(-m,-m+1),D(m,m+1).考慮方程組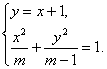 消去y,得(m-1)x2+m(x+1)2=m(m-1).整理得(2m-1)x2+2mx+2m-m2=0,Δ=4m2-4(2m-1)(2m-m2)=8m(m-1)2.
消去y,得(m-1)x2+m(x+1)2=m(m-1).整理得(2m-1)x2+2mx+2m-m2=0,Δ=4m2-4(2m-1)(2m-m2)=8m(m-1)2.
∵2≤m≤5,∴Δ>0恒成立,xB+xC=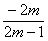 .又∵A、B、C、D都在直線y=x+1上,
.又∵A、B、C、D都在直線y=x+1上,
∴|AB|=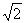 |xB-xA|=
|xB-xA|=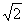 (xB-xA).同理|CD|=
(xB-xA).同理|CD|=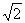 (xD-xC).
(xD-xC).
∴||AB|-|CD||=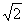 |xB-xA-xD+xC|=
|xB-xA-xD+xC|= |(xB+xC)-(xA+xD)|.
|(xB+xC)-(xA+xD)|.
又∵xA=-m,xD=m,
∴xA+xD=0.∴||AB|-|CD||=|xB+xC|·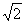 =|
=|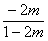 |·
|·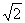 =
=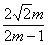 (2≤m≤5).
(2≤m≤5).
故f(m)= 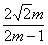 (m∈[2,5]).
(m∈[2,5]).

![]() =1(2≤m≤5),過其左焦點且斜率為1的直線與橢
=1(2≤m≤5),過其左焦點且斜率為1的直線與橢![]() ,即x=±m,∴A(-m,-m+1),D(m,m+1).考慮方程組
,即x=±m,∴A(-m,-m+1),D(m,m+1).考慮方程組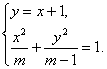 消去y,得(m-1)x2+m(x+1)2=m(m-1).整理得(2m-1)x2+2mx+2m-m2=0,Δ=4m2-4(2m-1)(2m-m2)=8m(m-1)2.
消去y,得(m-1)x2+m(x+1)2=m(m-1).整理得(2m-1)x2+2mx+2m-m2=0,Δ=4m2-4(2m-1)(2m-m2)=8m(m-1)2.![]() .又∵A、B、C、D都在直線y=x+1上,
.又∵A、B、C、D都在直線y=x+1上,![]() |xB-xA|=
|xB-xA|=![]() (xB-xA).同理|CD|=
(xB-xA).同理|CD|=![]() (xD-xC).
(xD-xC).![]() |xB-xA-xD+xC|=
|xB-xA-xD+xC|=![]() |(xB+xC)-(xA+xD)|.
|(xB+xC)-(xA+xD)|.![]() =|
=|![]() |·
|·![]() =
=![]() (2≤m≤5).
(2≤m≤5).![]() (m∈[2,5]).
(m∈[2,5]).

 如圖,已知橢圓
如圖,已知橢圓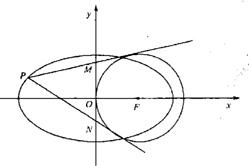 如圖,已知橢圓
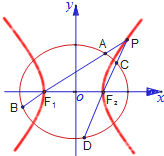
如圖,已知橢圓 (2012•湖南模擬)選做題(請考生在第16題的三個小題中任選兩題作答,如果全做,則按前兩題記分,要寫出必要的推理與演算過程)
(2012•湖南模擬)選做題(請考生在第16題的三個小題中任選兩題作答,如果全做,則按前兩題記分,要寫出必要的推理與演算過程) 如圖,已知橢圓Γ:
如圖,已知橢圓Γ: