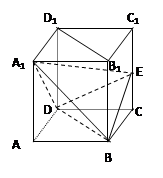試題分析:A不正確,m∥n,m?α,由于n可能在α內,故推不出n∥α;
對于B,由于當滿足

⊥β,m∥

,則m與β可能斜交,因此錯誤
對于C,由于;

⊥β,m⊥β,則m∥

,也可能m在

內,錯誤
對于D,則根據(jù)m⊥n,m⊥

,n⊥β,則

⊥β,符合面面垂直的判定定理,成立,故選D.
點評:本題考查線面,線線、面面的平行關系的判斷,重點考查了空間的感知能力與空間中線面之間位置關系的判斷能力.
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:解答題
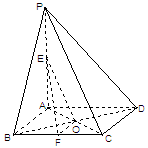
如圖,在四棱錐
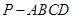
中,
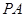
⊥平面

,
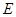
為
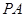
的中點,

為
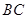
的中點,底面

是菱形,對角線
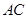
,

交于點
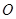
.
求證:(1)平面
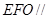
平面
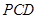
;
(2)平面

⊥平面

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題12分)
如圖,在
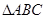
中,
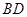
為
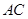
邊上的高,

,沿
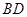
將
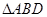
翻折,使得
得幾何體


(Ⅰ)求證:
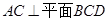
;
(Ⅱ)求點D到面ABC的距離。
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題共12分)
如圖,在四棱錐
P-
ABCD中,底面
ABCD為直角梯形,
AD//
BC,∠
ADC=90°,平面
PAD⊥底面
ABCD,
Q為
AD的中點,
M是棱
PC上的點,
PA=
PD=2,
BC=
 AD
AD=1,
CD=
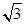
.
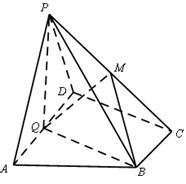
(1)求證:平面
PQB⊥平面
PAD;
(2)若二面角M-BQ-C為30°,設PM=tMC,試確定t的值.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(12分)如圖,在正方體ABCD-A
1B
1C
1D
1中,E、F、G分別是CB、CD、CC
1的中點,
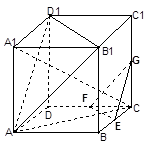
(1)求證:平面A B
1D
1∥平面EFG;
(2)求證:平面AA
1C⊥面EFG.
(3)求異面直線AC與A
1B所成的角
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設m,n是異面直線,則(1)一定存在平面α,使m

α,且n∥α;(2)一定存在平面α,使m

α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距離相等;(4)一定存在無數(shù)對平面α和β,使m

α,n

β且α⊥β。上述4個命題中正確命題的序號是( )
| A.(1)(2)(3) | B.(1)(2)(4) | C.(1)(3)(4) | D.(1)(4) |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)
如圖,邊長為a的正方體ABCD-A
1B
1C
1D
1中,E為CC
1的中點.
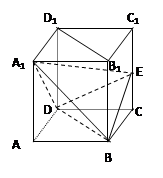
(1)求直線A
1E與平面BDD
1B
1所成的角的正弦值
(2)求點E到平面A
1DB的距離
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知
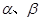
表示兩個互相垂直的平面,
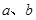
表示一對異面直線,則
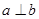
的一個充分條件是( )
A.
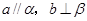
B.
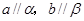
C.
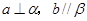
D.
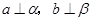
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
設
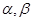
為使互不重合的平面,
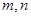
是互不重合的直線,給出下列四個命題:
①

②

③

④若
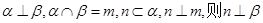
;
其中正確命題的序號為
.
查看答案和解析>>

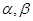 是兩個不同的平面,則下列命題中正確的是
是兩個不同的平面,則下列命題中正確的是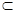
 ,則n∥
,則n∥ ;
;  ⊥β,m∥
⊥β,m∥ ,則m⊥β;
,則m⊥β; ⊥β,m⊥β,則m∥
⊥β,m⊥β,則m∥ ;
; ,n⊥β,則
,n⊥β,則 ⊥β
⊥β AD=1,CD=
AD=1,CD=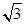 .
.
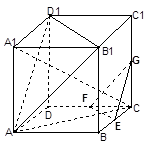
 α,且n∥α;(2)一定存在平面α,使m
α,且n∥α;(2)一定存在平面α,使m α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距離相等;(4)一定存在無數(shù)對平面α和β,使m
α,且n⊥α;(3)一定存在平面γ,使得m,n到平面γ距離相等;(4)一定存在無數(shù)對平面α和β,使m α,n
α,n β且α⊥β。上述4個命題中正確命題的序號是( )
β且α⊥β。上述4個命題中正確命題的序號是( )