Question

【題目】設函數f（x）=x3﹣12x+4，x∈R．
（1）求f（x）的單調區間和極值；
（2）若關于x的方程f（x）=a有3個不同實根，求實數a的取值范圍．

Answer 1

【答案】
（1）解：∵f（x）=x3﹣12x+4，

∴f′（x）=3x2﹣12=3（x+2）（x﹣2）

令f′（x）=0得：x1=﹣2，x2=2

當x變化時，f'（x），f（x）的變化情況如下表：

x	（﹣∞，﹣2）	﹣2	（﹣2，2）	2	（2，+∞）
f'（x）	+	0	﹣	0	+
f（x）	增	極大	減	極小	增

所以f（x）的增區間是（﹣∞，﹣2）和（2，+∞），減區間是（﹣2，2）；

當x=﹣2時，f（x）取得極大值，極大值f（﹣2）=20；

當x=2時，f（x）取得極小值，極小值f（2）=﹣12

（2）解：由（1）可知y=f（x）圖象的大致形狀及走向：

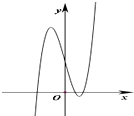
∴當﹣12＜a＜20時，直線y=a與y=f（x）的圖象有3個不同交點，

即當﹣12＜a＜20時方程f（x）=a有三解

【解析】（1）求出函數的導函數，進而分析導函數在不同區間上的符號，進而根據導函數為正，對應函數的單調遞增區間；導函數為負，對應函數的單調遞減區間，得到f（x）的單調區間；再由左增右減對應函數的極大值，左減右增，對應函數的極小值，得到f（x）的極值；（2）由（1）作出函數f（x）的草圖，進而得到方程f（x）=a有3個不同實根，可轉化為a值，介于函數的兩極值之間，進而得到實數a的取值范圍．
【考點精析】關于本題考查的利用導數研究函數的單調性和函數的極值與導數，需要了解一般的,函數的單調性與其導數的正負有如下關系： 在某個區間內，(1)如果，那么函數在這個區間單調遞增；(2)如果，那么函數在這個區間單調遞減；求函數的極值的方法是:（1）如果在附近的左側,右側,那么是極大值（2）如果在附近的左側,右側,那么是極小值才能得出正確答案．