
小區統計部門隨機抽查了區內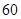 名網友4月1日這天的網購情況,得到如下數據統計表(圖(1)).網購金額超過
名網友4月1日這天的網購情況,得到如下數據統計表(圖(1)).網購金額超過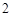 千元的顧客被定義為“網購紅人”,網購金額不超過
千元的顧客被定義為“網購紅人”,網購金額不超過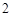 千元的顧客被定義為“非網購紅人”.已知“非網購紅人”與“網購紅人”人數比恰為
千元的顧客被定義為“非網購紅人”.已知“非網購紅人”與“網購紅人”人數比恰為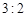 .
.
(1)確定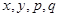 的值,并補全頻率分布直方圖(圖(2)).
的值,并補全頻率分布直方圖(圖(2)).
(2)為進一步了解這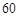 名網友的購物體驗,從“非網購紅人”和“網購紅人”中用分層抽樣的方法確定
名網友的購物體驗,從“非網購紅人”和“網購紅人”中用分層抽樣的方法確定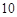 人,若需從這
人,若需從這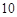 人中隨機選取
人中隨機選取 人進行問卷調查,設
人進行問卷調查,設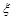 為選取的
為選取的 人中“網購紅人”的人數,求
人中“網購紅人”的人數,求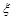 的分布列和數學期望.
的分布列和數學期望.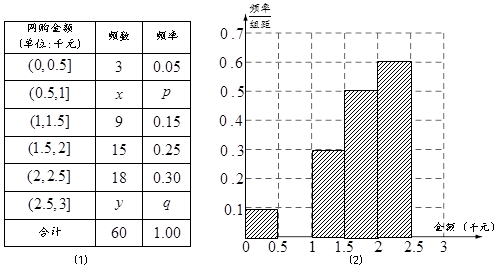
(1) ,
, ,補全頻率分布直方圖如圖所示.
,補全頻率分布直方圖如圖所示.
(2)分布列為
 .
.
解析試題分析:(1) “非網購紅人”與“網購紅人”人數比恰為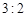 ,又總人數為60,由此可得一個方程組,解這個方程組可得:
,又總人數為60,由此可得一個方程組,解這個方程組可得: ,進而可得:
,進而可得: .這樣便可補全頻率分布直方圖;
.這樣便可補全頻率分布直方圖;
(2)選出的人中,“網購紅人”有4人,“非網購紅人”有6人,從中取3人,故“網購紅人”的人數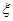 的可能取值為0,1,2,3,這是一個超幾何分布,由超幾何分布的概率公式可得其分布列,進而求得其期望.
的可能取值為0,1,2,3,這是一個超幾何分布,由超幾何分布的概率公式可得其分布列,進而求得其期望.
(1) “非網購紅人”與“網購紅人”人數比恰為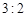 ,所以
,所以 ,
,
又 ,解這個方程組得:
,解這個方程組得: .從而可得:
.從而可得: .
.
補全頻率分布直方圖如圖所示:
(2)選出的人中,“網購紅人”有4人,“非網購紅人”有6人,故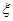 的可能取值為0,1,2,3,
的可能取值為0,1,2,3,
因為 ,
, ,
,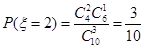 ,
, ,
,
所以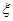 的分布列為:
的分布列為:
 .
.
考點:1、頻率分布直方圖;2、隨機變量的分布列及期望.


科目:高中數學 來源: 題型:解答題
某高校共有學生15 000人,其中男生10 500人,女生4 500人,為調查該校學生每周平均體育運動的情況,采用分層抽樣的方法,收集300位學生每周平均體育運動時間的樣本數據(單位:小時).
(1)應收集多少位女生的樣本數據?
(2)根據這300個樣本數據,得到學生每周平均體育運動時間的頻率分布直方圖(如圖所示),其中樣本數據的分組區間為:[0,2],(2,4], (4,6], (6,8], (8,10], (10,12],估計該校學生每周平均體育運動時間超過4小時的概率;
(3)在樣本數據中,有60位女生的每周平均體育運動時間超過4小時,請完成每周平均體育運動時間與性別列聯表,并判斷是否有95%的把握認為“該校學生的每周平均體育運動時間與性別有關”.
附:

| P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)一工廠生產甲、乙、丙三種樣式的杯子,每種樣式均有 和
和 兩種型號,某天的產量如右表(單位:個):按樣式分層抽樣的方法在這個月生產的杯子中抽取
兩種型號,某天的產量如右表(單位:個):按樣式分層抽樣的方法在這個月生產的杯子中抽取 個,其中有甲樣式杯子
個,其中有甲樣式杯子 個.
個.
| 型號 | 甲樣式 | 乙樣式 | 丙樣式 |
 |  |  |  |
 |  |  |  |
 的值;
的值;  的樣本,從這個樣本中任取
的樣本,從這個樣本中任取 個杯子,求至少有
個杯子,求至少有 個
個 杯子的概率.
杯子的概率.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品的廣告費用支出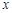 (萬元)與銷售額
(萬元)與銷售額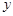 (萬元)之間有如下的對應數據:
(萬元)之間有如下的對應數據:
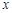 | 2 | 4 | 5 | 6 | 8 |
 | 30 | 40 | 60 | 50 | 70 |
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
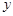 的值.
的值. ,其中
,其中 .
.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為了了解高一年級學生的身高情況,某校按10%的比例對全校800名高一年級學生按性別進行抽樣檢查,得到如下頻數分布表:
表1:男生身高頻數分布表
| 身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190] |
| 頻數 | 2 | 5 | 14 | 13 | 4 | 2 |
| 身高(cm) | [150,155) | [150,160) | [160,165) | [165,170) | [170,175) | [175,180] |
| 頻數 | 2 | 12 | 16 | 6 | 3 | 1 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
以下莖葉圖記錄了甲,乙兩組各三名同學在期末考試中的數學成績(十位數字為莖,個位數字為葉).乙組記錄中有一個數字模糊,無法確認,假設這個數字具有隨機性,并在圖中以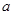 表示.
表示.
(1)若甲,乙兩個小組的數學平均成績相同,求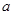 的值;
的值;
(2)當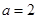 時,分別從甲,乙兩組同學中各隨機選取一名同學,求這兩名同學的數學成績之差的絕對值不超過2分的概率.
時,分別從甲,乙兩組同學中各隨機選取一名同學,求這兩名同學的數學成績之差的絕對值不超過2分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某中學高三文科班學生參加了數學與地理水平測試,學校從測試合格的學生中隨機抽取100人的成績進行統計分析.抽取的100人的數學與地理的水平測試成績如下表: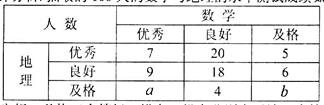
成績分為優秀、良好、及格三個等級,橫向、縱向分別表示地理成績與數學成績,例如:表中數學成績為良好的共有20+18+4=42人.
(1)若在該樣本中,數學成績優秀率為30%,求a,b的值;
(2)若樣本中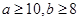 ,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
,求在地理成績及格的學生中,數學成績優秀的人數比及格的人數少的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某種產品的廣告費支出x(單位:百萬元)與銷售額y(單位:百萬元)之間有如下對應數據:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
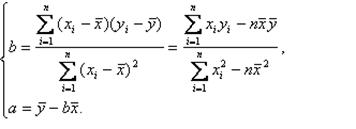
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為調查某地區老年人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
| 性別 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥x0) | 0.050 | 0.010 | 0.001 |
| x0 | 3.841 | 6.635 | 10.828 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com