【答案】
分析:(1)A(x
1,y
1)、B(x
2,y
2)根據(jù)|OA|=|OB|可得x
12+y
12=x
22+y
22.由于A,B都在拋物線上進而滿足y
12=2px
1,y
22=2px
2,整理可得(x
2-x
1)(x
1+x
2+2p)=0.根據(jù)x
1、x
2與p同號可知x
1+x
2+2p≠0進而可得x
1=x
2.根據(jù)拋物線對稱性,知點A、B關于x軸對稱.
(2)由(1)可知∠AOx=30°,進而根據(jù)拋物線和直線方程求得點A的坐標,設外接圓方程把點A代入即可求得d,方程可得.
解答:(1)證明:設A(x
1,y
1)、B(x
2,y
2),
∵|OA|=|OB|,∴x
12+y
12=x
22+y
22.
又∵y
12=2px
1,y
22=2px
2,
∴x
22-x
12+2p(x
2-x
1)=0,
即(x
2-x
1)(x
1+x
2+2p)=0.
又∵x
1、x
2與p同號,∴x
1+x
2+2p≠0.
∴x
2-x
1=0,即x
1=x
2.
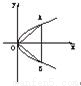
由拋物線對稱性,知點A、B關于x軸對稱.
(2)解:由(1)知∠AOx=30°,則y
2=2px,x=6p,
∴y=
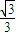
x,y=2

p.
∴A(6p,2
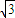
p).
△AOB外接圓過原點O,且圓心在x軸上,可設其方程為x
2+y
2+dx=0.
將點A(6p,2
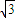
p)代入,得d=-8p.
故△AOB外接圓方程為x
2+y
2-8px=0.
點評:本題主要考查拋物線的應用和用待定系數(shù)法求得曲線方程的問題.是高考中經(jīng)常考的題目,應加強訓練.

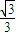 x,y=2
x,y=2 p.
p.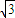 p).
p).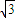 p)代入,得d=-8p.
p)代入,得d=-8p.
