
分析 (1)根據函數的奇偶性的定義即可討論得到結論,
(2)先化簡g(x),再根據導數和函數單調性的關系,求導分離參數,求出函數的最值,問題得以解決.
解答 解:(1)∵f(x)=ax2+(a-1)x+a,
∴f(-x)=ax2-(a-1)x+a,
若f(-x)=f(x),即ax2-(a-1)x+a=ax2+(a-1)x+a,
解得a=1,此時函數為偶函數,
若f(-x)=-f(x),即ax2-(a-1)x+a=-ax2-(a-1)x-a,
解得a=0,此時函數為奇函數,
當a≠1且a≠0時,函數為非奇非偶函數,
(2)∵$g(x)=f(x)+\frac{{1-({a-1}){x^2}}}{x}$=ax2+(a-1)x+a+$\frac{1}{x}$-(a-1)x=ax2+a+$\frac{1}{x}$,
∴g′(x)=2ax-$\frac{1}{x}$>0,在(2,3)上恒成立,
∴2a>$\frac{1}{{x}^{2}}$,
∴y=$\frac{1}{{x}^{2}}$在(2,3)上為減函數,
∴y>$\frac{1}{4}$,
∴2a≥$\frac{1}{4}$,
∴a≥$\frac{1}{8}$,
故a的取值范圍為[$\frac{1}{8}$,+∞).
點評 本題主要考查了函數的單調性、奇偶性,利用了分類討論的思想以及導數和函數的單調性的關系,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | ②③④ | B. | ①②③ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
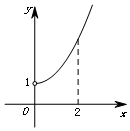 已知函數y=f(x)(x∈R)是奇函數,其部分圖象如圖所示,則在(-2,0)上與函數f(x)的單調性相同的是( )
已知函數y=f(x)(x∈R)是奇函數,其部分圖象如圖所示,則在(-2,0)上與函數f(x)的單調性相同的是( )| A. | y=x2+1 | B. | y=log2|x| | ||
| C. | y=$\left\{\begin{array}{l}{{e}^{x}(x≥0)}\\{{e}^{-x}(x<0)}\end{array}\right.$ | D. | y=|x+2| |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | a2+b2>2ab | B. | $a+b≥2\sqrt{ab}$ | C. | $\frac{b}{a}+\frac{a}{b}$≥2 | D. | $\frac{1}{a}+\frac{1}{b}≥\frac{2}{{\sqrt{ab}}}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com