【答案】
分析:在三角函數式中先把X的系數用誘導公式變為正,表現出來是負號提前,這樣要求函數的增區間變成了去掉負號后的函數的減區間,據正弦函數的減區間求出結果,寫出在規定的范圍的區間.
解答:解:∵y=2sin(

-2x)=-2sin(2x-

),
∴只要求y=2sin(2x-

)的減區間,
∵y=sinx的減區間為【2kπ+

,2kπ+

],
∴2x-

∈[2kπ+

,2k

],
∴x

,
∵x∈[0,π],
∴

,
故答案為:【


】.
點評:在三角函數單調性運算時,若括號中給出的角自變量的系數為負,一定要先用誘導公式把負號變正,否則,計算出的單調區間剛好相反,原因是復合函數單調性引起的.

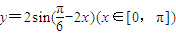 為增函數的區間是 .
為增函數的區間是 .