
| 2 |
| π |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
| MM1 |
| AB |
| FM |
| FA |
| CN |
| CE |
| NN1 |
| EF |
| CN |
| NE |
| FM |
| MA |
| FG |
| GE |
| ||
| 2 |
| 1 |
| 2 |
(
|
| ||
| 2 |
| ||
| 2 |
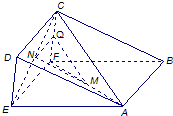
| QM2+MN2-NQ2 |
| 2MN•QM |
| ||
| 3 |
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| MN |
| 1 |
| 2 |
| 1 |
| 2 |
| AC |
| MN |
| 1 | ||||||
|
| ||
| 3 |
| ||
| 3 |


科目:高中數(shù)學(xué) 來源: 題型:
| 2 |
| π |
| 2 |

| ||
| 2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
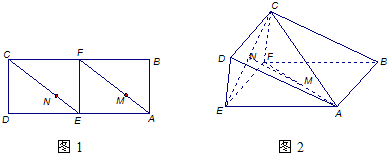
 (2013•日照一模)已知長方形EFCD,|EF|=2,|FC|=
(2013•日照一模)已知長方形EFCD,|EF|=2,|FC|=
| ||
| 2 |
| FA |
| FB |
| TA |
| TB |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:《立體幾何》2013年廣東省十二大市高三二模數(shù)學(xué)試卷匯編(理科)(解析版) 題型:解答題
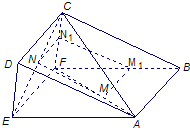
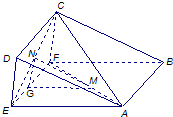
 .把長方形ABCD沿EF折成大小為θ的二面角A-EF-C,如圖(2)所示,其中
.把長方形ABCD沿EF折成大小為θ的二面角A-EF-C,如圖(2)所示,其中
 .時,求異面直線MN與AC所成角的余弦值.
.時,求異面直線MN與AC所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2013年廣東省揭陽市高考數(shù)學(xué)二模試卷(理科)(解析版) 題型:解答題
 .把長方形ABCD沿EF折成大小為θ的二面角A-EF-C,如圖(2)所示,其中
.把長方形ABCD沿EF折成大小為θ的二面角A-EF-C,如圖(2)所示,其中
 .時,求異面直線MN與AC所成角的余弦值.
.時,求異面直線MN與AC所成角的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com