
(2007
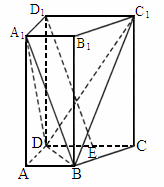
山東,19)如下圖,在直四棱柱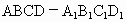 中,已知
中,已知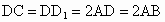 ,AD⊥DC,AB∥DC.
,AD⊥DC,AB∥DC.
(1)
設E是DC的中點,求證: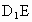 ∥平面
∥平面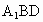 ;
;
(2)
求二面角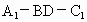 的余弦值.
的余弦值.
|
解析:解法一: (1)連接BE,則四邊形DABE為正方形,
∴ 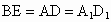 ,且 ,且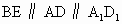 , ,
∴四邊形 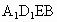 為平行四邊形. 為平行四邊形.
∴ 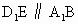 . .
又 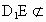 平面 平面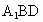 , ,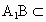 平面 平面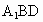 , ,
∴  . .
(2) 以D為原點,DA,DC,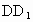 所在直線分別為x軸,y軸,z軸,建立如圖所示的空間直角坐標系,不妨設DA=1,則D(0,0,0),A(1,0,0),B(1,1,0), 所在直線分別為x軸,y軸,z軸,建立如圖所示的空間直角坐標系,不妨設DA=1,則D(0,0,0),A(1,0,0),B(1,1,0),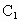 (0,2,2), (0,2,2),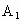 (1,0,2), (1,0,2),
∴ 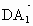 =(1,0,2), =(1,0,2),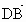 =(1,1,0). =(1,1,0).
設 n=(x,y,z)為平面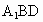 的一個法向量, 的一個法向量,
由 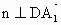 , ,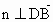 , ,
得 
取 z=1,則n=(-2,2,1).又 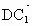 =(0,2,2), =(0,2,2),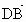 =(1,1,0), =(1,1,0),
設 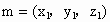 為平面 為平面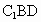 的一個法向量,由 的一個法向量,由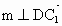 , ,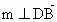 , ,
得 
取 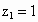 ,則m=(1,-1,1). ,則m=(1,-1,1).
設 m與n的夾角為α,二面角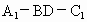 為θ,顯然θ為銳角, 為θ,顯然θ為銳角,
∴ 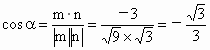 .∴ .∴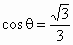 . .
即所求二面角 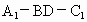 的余弦值為 的余弦值為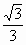 . .
解法二: (1)以D為原點,DA,DC,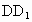 所在直線分別為x軸,y軸,z軸,建立如圖所示的空間直角坐標系, 所在直線分別為x軸,y軸,z軸,建立如圖所示的空間直角坐標系,
設 DA=a,由題意知:D(0 ,0,0),A(a,0,0),B(a,a,0),C(0,2a,0),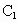 (0,2a,2a), (0,2a,2a),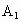 (a,0,2a), (a,0,2a), (0,0,2a),E(0,a,0), (0,0,2a),E(0,a,0),
∴ 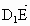 =(0,a,-2a), =(0,a,-2a),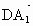 =(a,0,2a), =(a,0,2a),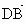 =(a,a,0). =(a,a,0).
又 (0,a,-2a)=(a,a,0)-(a,0,2a),∴ 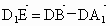 . .
∵ 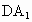 ,DB ,DB 平面 平面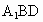 , ,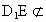 平面 平面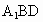 , ,
∴  . .
(2) 取DB的中點F,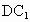 的中點M,連接 的中點M,連接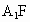 ,FM,由(1)及題意得知 ,FM,由(1)及題意得知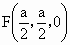 ,M(0,a,a), ,M(0,a,a),
∴ 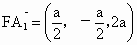 , ,
∴ 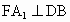 ,FM⊥DB. ,FM⊥DB.
∴ 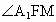 為所求二面角的平面角. 為所求二面角的平面角.
∴ 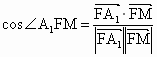
所以二面角 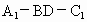 的余弦值為 的余弦值為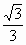 . .
解法三: (1)證明:如解法一圖,連接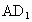 ,AE, ,AE,
設 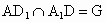 ,AE∩BD=F,連接GF, ,AE∩BD=F,連接GF,
由題意知 G是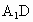 的中點,又E是CD的中點, 的中點,又E是CD的中點,
∴四邊形 ABED是平行四邊形,故F是AE的中點,∴在 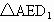 中, 中,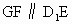 , ,
又 GF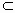 平面 平面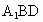 , ,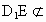 平面 平面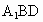 , ,
∴ 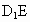 ∥平面 ∥平面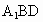 . .
(2) 如圖,在四邊形ABCD中,設AD=a,
∵ AB=AD,AD⊥DC,AB∥DC,∴ AD⊥AB.故  ,由(1)得 ,由(1)得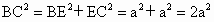 ,DC=2a, ,DC=2a,
∴∠ DBC=90°,即 BD⊥BC.又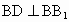 , ,
∴ BD⊥平面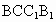 ,又 ,又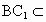 平面 平面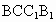 ,∴ ,∴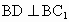 . .
取 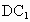 的中點M,連接 的中點M,連接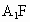 ,FM,由題意知 ,FM,由題意知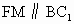 , ,
∴ FM⊥BD.又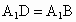 ,∴ ,∴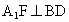 . .
∴ 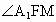 為二面角 為二面角 的平面角, 的平面角,
連接 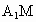 ,在 ,在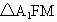 中,由題意知: 中,由題意知:
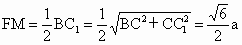 , ,
取 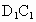 的中點H,連接 的中點H,連接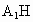 ,HM, ,HM,
在 Rt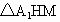 中,∵ 中,∵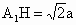 ,HM=a, ,HM=a,
∴ 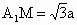 . .
∴ 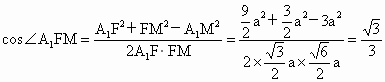 . .
∴二面角 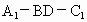 的余弦值為 的余弦值為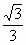 . . |


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:高中數學 來源: 題型:013
(2007
山東,8)某班50名學生在一次百米測試中,成績全部介于13秒與19秒之間,將測試結果按如下方式分成六組:第一組,成績大于等于13秒且小于14秒;第二組,成績大于等于14秒且小于15秒;……第六組,成績大于等于18秒且小于等于19秒.如圖所示是按上述分組方法得到的頻率分布直方圖.設成績小于17秒的學生人數占全班總人數的百分比為x,成績大于等于15秒且小于17秒的學生人數為y,則從頻率分布直方圖中可分析出x和y分別為
[
]|
A .0.9,35 |
B .0.9,45 |
C .0.1,35 |
D .0.1,45 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com