
【題目】已知![]() ,設
,設![]() ,且
,且![]() ,記
,記![]() ;
;
(1)設![]() ,其中
,其中![]() ,試求
,試求![]() 的單調區間;
的單調區間;
(2)試判斷弦![]() 的斜率
的斜率![]() 與
與![]() 的大小關系,并證明;
的大小關系,并證明;
(3)證明:當![]() 時,
時,![]() .
.
【答案】(1)見解析;(2)見證明;(3)見證明
【解析】
(1)![]() (
(![]() ),對其求導,討論
),對其求導,討論![]() 的范圍即可判斷
的范圍即可判斷![]() 的單調區間;(2)
的單調區間;(2)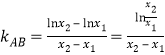 ,
,![]() ,二者作差,
,二者作差,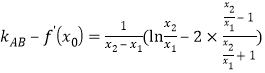 ,令
,令![]() ,構造函數
,構造函數![]() ,通過求導可判斷
,通過求導可判斷![]() 的單調性,從而可得到
的單調性,從而可得到![]() ,即可判斷
,即可判斷![]() ;(3)當
;(3)當![]() 時,原不等式等價于
時,原不等式等價于![]() ,由(2)知
,由(2)知![]() ,即證
,即證![]() ,轉化為
,轉化為![]() ,構造函數
,構造函數![]() ,通過求導可判斷它的單調性進而得到
,通過求導可判斷它的單調性進而得到![]() ,從而證明了結論。
,從而證明了結論。
(1)![]() (
(![]() ),
),![]()
若![]() ,則
,則![]() ,
,![]() 是
是![]() 上的增函數,
上的增函數,
若![]() ,則
,則![]() 的增區間為
的增區間為![]() ,減區間為
,減區間為![]() .
.
(2)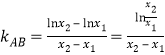 ,
,![]() ,
,
則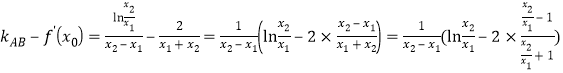 ,
,
令![]() ,則
,則![]() ,
,
令![]() ,
,![]() ,
,
而![]() ,則
,則![]() 在
在![]() 單調遞增,且恒為正,
單調遞增,且恒為正,
又因為![]() ,所以
,所以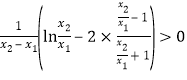 ,即
,即![]() .
.
(3)當![]() 時,原不等式等價于
時,原不等式等價于![]() ,由(2)知
,由(2)知![]() ,即證
,即證![]() ,轉化為
,轉化為![]() .
.
令![]() ,
,![]() ,
,
令![]() ,則
,則![]() ,
,
當![]() 時,
時,![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
則![]() ,故
,故![]() 在
在![]() 上單調遞增,
上單調遞增,
則![]() ,故
,故![]() 時,
時,![]() 成立,即當
成立,即當![]() 時,
時,![]() .
.


 尖子生新課堂課時作業系列答案
尖子生新課堂課時作業系列答案 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:高中數學 來源: 題型:
【題目】2018年6月份上合峰會在青島召開,面向高校招募志愿者,中國海洋大學海洋環境學院的8名同學符合招募條件并審核通過,其中大一、大二、大三、大四每個年級各2名.若將這8名同學分成甲乙兩個小組,每組4名同學,其中大一的兩名同學必須分到同一組,則分到乙組的4名同學中恰有2名同學是來自于同一年級的分組方式共有__________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有![]() ,
,![]() ,…,
,…,![]() 這5個球隊進行單循環比賽(全部比賽過程中任何一隊都要分別與其他各隊比賽一場且只比賽一場).當比賽進行到一定階段時,統計
這5個球隊進行單循環比賽(全部比賽過程中任何一隊都要分別與其他各隊比賽一場且只比賽一場).當比賽進行到一定階段時,統計![]() ,
,![]() ,
,![]() ,
,![]() 這4個球隊已經賽過的場數分別為:
這4個球隊已經賽過的場數分別為:![]() 隊4場,
隊4場,![]() 隊3場,
隊3場, ![]() 隊2場,
隊2場,![]() 隊1場,則
隊1場,則![]() 隊比賽過的場數為( )
隊比賽過的場數為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“十三五”規劃確定了到2020年消除貧困的宏偉目標,打響了精準扶貧的攻堅戰,為完成脫貧任務,某單位在甲地成立了一家醫療器械公司吸納附近貧困村民就工,已知該公司生產某種型號醫療器械的月固定成本為20萬元,每生產1千件需另投入5.4萬元,設該公司一月內生產該型號醫療器械x千件且能全部銷售完,每千件的銷售收入為![]() 萬元,已知
萬元,已知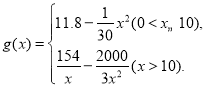
(1)請寫出月利潤y(萬元)關于月產量x(千件)的函數解析式;
(2)月產量為多少千件時,該公司在這一型號醫療器械的生產中所獲月利潤最大?并求出最大月利潤(精確到0.1萬元).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的右焦點為
的右焦點為![]() ,上頂點為
,上頂點為![]() ,直線
,直線![]() 的斜率為
的斜率為![]() ,且原點到直線
,且原點到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若不經過點![]() 的直線
的直線![]() :
:![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,且與圓
兩點,且與圓![]() 相切.試探究
相切.試探究![]() 的周長是否為定值,若是,求出定值;若不是,請說明理由.
的周長是否為定值,若是,求出定值;若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com