解:(1)設0<a≤b≤c,a+b>c,欲證明
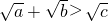
,
只需證明

,成立.①是“保三角形函數”;
取
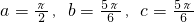
,而sinb+sinc=sina,②不是“保三角形函數”;
(2)M的最小值為2
(i)首先證明當M≥2時,函數h(x)=lnx (x∈[M,+∞))是保三角形函數.
對任意一個三角形三邊長a,b,c∈[M,+∞),且a+b>c,b+c>a,c+a>b,
則h(a)=lna,h(b)=lnb,h(c)=lnc.
因為a≥2,b≥2,a+b>c,所以(a-1)(b-1)≥1,所以ab≥a+b>c,所以lnab>lnc,
即lna+lnb>lnc.
同理可證明lnb+lnc>lna,lnc+lna>lnb.
所以lna,lnb,lnc是一個三角形的三邊長.
故函數h(x)=lnx (x∈[M,+∞),M≥2),是保三角形函數…13分
(ii)其次證明當0<M<2<M<2時,H(X)=LNX (x∈[M,+∞))不是保三角形函數,h(x)=lnx (x∈[M,+∞))不是保三角形函數
因為0<M<2,所以M+M=2M>M
2,所以M,M,M
2是某個三角形的三條邊長,
而lnM+lnM=2lnM=lnM
2,所以lnM,lnM,lnM
2不能為某個三角形的三邊長,所以h(x)=lnx 不是保三角形函數.
所以,當M<2時,h(x)=lnx (x∈[M,+∞))不是保三角形函數.
綜上所述:M的最小值為2
分析:(1)任給三角形,設它的三邊長分別為a,b,c,則a+b>c,不妨假設a≤c,b≤c,我們判斷f(a),f(b),f(c)是否滿足任意兩數之和大于第三個數,即任意兩邊之和大于第三邊;
(2)要利用“保三角形函數”的概念,求M的最小值,首先證明當M≥2時,函數h(x)=lnx (x∈[M,+∞))是保三角形函數,然后證明當0<M<2<M<2時,H(X)=LNX (x∈[M,+∞))不是保三角形函數,h(x)=lnx (x∈[M,+∞))不是保三角形函數,從而求出所求.
點評:要想判斷f(x)為“保三角形函數”,要經過嚴密的論證說明f(x)滿足“保三角形函數”的概念,但要判斷f(x)不為“保三角形函數”,僅須要舉出一個反例即可,屬于創新題.

 ; ②g(x)=sinx (x∈(0,π)).
; ②g(x)=sinx (x∈(0,π)).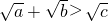 ,
, ,成立.①是“保三角形函數”;
,成立.①是“保三角形函數”;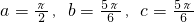 ,而sinb+sinc=sina,②不是“保三角形函數”;
,而sinb+sinc=sina,②不是“保三角形函數”;
