
【題目】已知A(1,0,0),B(0,1,0),C(0,0,2).
(1)若![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,求點D的坐標;
,求點D的坐標;
(2)問是否存在實數α,β,使得![]() =α
=α![]() +β
+β![]() 成立?若存在,求出α,β的值;若不存在,說明理由.
成立?若存在,求出α,β的值;若不存在,說明理由.
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】
(1) 設D(x,y,z),由![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,得到
,得到![]() 解方程組即得解.(2) 假設存在實數α,β,使得
解方程組即得解.(2) 假設存在實數α,β,使得![]() =α
=α![]() +β
+β![]() 成立,則有(-1,0,2)=α(-1,1,0)+β(0,-1,2)=(-α,α-β,2β),所以
成立,則有(-1,0,2)=α(-1,1,0)+β(0,-1,2)=(-α,α-β,2β),所以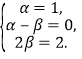 解之即得解.
解之即得解.
(1)設D(x,y,z),則![]() =(-x,1-y,-z),
=(-x,1-y,-z),![]() =(-1,0,2),
=(-1,0,2),
![]() =(-x,-y,2-z),
=(-x,-y,2-z),![]() =(-1,1,0).
=(-1,1,0).
因為![]() ∥
∥![]() ,
,![]() ∥
∥![]() ,
,
所以![]()
解得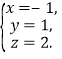
即D(-1,1,2).
(2)依題意![]() =(-1,1,0),
=(-1,1,0),![]() =(-1,0,2),
=(-1,0,2),![]() =(0,-1,2).
=(0,-1,2).
假設存在實數α,β,使得![]() =α
=α![]() +β
+β![]() 成立,則有(-1,0,2)=α(-1,1,0)+β(0,-1,2)=(-α,α-β,2β).
成立,則有(-1,0,2)=α(-1,1,0)+β(0,-1,2)=(-α,α-β,2β).
所以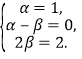 故存在α=β=1,使得
故存在α=β=1,使得![]() =α
=α![]() +β
+β![]() 成立.
成立.


 階梯計算系列答案
階梯計算系列答案科目:高中數學 來源: 題型:
【題目】已知函數 , 其中a∈R.若對任意的非零實數x1 , 存在唯一的非零實數x2(x1≠x2),使得f(x1)=f(x2)成立,則k的取值范圍為( )
, 其中a∈R.若對任意的非零實數x1 , 存在唯一的非零實數x2(x1≠x2),使得f(x1)=f(x2)成立,則k的取值范圍為( )
A.k≤0
B.k≥8
C.0≤k≤8
D.k≤0或k≥8
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知F是拋物線y2=4x的焦點,點A,B在該拋物線上且位于x軸的兩側,OA⊥OB(其中O為坐標原點),則△AOB與△AOF面積之和的最小值是( )
A.16
B.8![]()
C.8![]()
D.18
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinx(sinx+![]() cosx).
cosx).
(1)求f(x)的最小正周期和最大值;
(2)在銳角三角形ABC中,角A,B,C的對邊分別為a,b,c,若f(![]() )=1,a=2
)=1,a=2![]() , 求三角形ABC面積的最大值.
, 求三角形ABC面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電視傳媒公司為了了解某類體育節目的收視情況,隨機抽取了100名觀眾進行調查,如圖是根據調查結果繪制的觀眾日均收看該類體育節目時間的頻率分布直方圖,其中收看時間分組區間是:[0,10),[10,20),[20,30),[30,40),[40,50),[50,60].則圖中x的值為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊邊長為1(百米)的正方形區域ABCD.在點A處有一個可轉動的探照燈,其照射角∠PAQ始終為45°(其中點P,Q分別在邊BC,CD上),設BP=t.
(I)用t表示出PQ的長度,并探求△CPQ的周長l是否為定值;
(Ⅱ)設探照燈照射在正方形ABCD內部區域的面積S(平方百米),求S的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,某自行車手從O點出發,沿折線O﹣A﹣B﹣O勻速騎行,其中點A位于點O南偏東45°且與點O相距20 ![]() 千米.該車手于上午8點整到達點A,8點20分騎至點C,其中點C位于點O南偏東(45°﹣α)(其中sinα=
千米.該車手于上午8點整到達點A,8點20分騎至點C,其中點C位于點O南偏東(45°﹣α)(其中sinα= ![]() ,0°<α<90°)且與點O相距5
,0°<α<90°)且與點O相距5 ![]() 千米(假設所有路面及觀測點都在同一水平面上).
千米(假設所有路面及觀測點都在同一水平面上).
(1)求該自行車手的騎行速度;
(2)若點O正西方向27.5千米處有個氣象觀測站E,假定以點E為中心的3.5千米范圍內有長時間的持續強降雨.試問:該自行車手會不會進入降雨區,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com