日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情

【題目】已知數列滿足且，設，.

（1）求；

（2）求的通項公式；

（3）求.

【答案】（1），，，；（2），；（3）.

【解析】

（1）依次代入計算，可求得；

（2）歸納出，并用數學歸納法證明；

（3）用裂項相消法求和，然后求極限．

（1）∵且，

∴，即，，，

，，，

，，，

∴；

（2）由（1）歸納：，

下面用數學歸納法證明：

1°n=1，n=2時，由（1）知成立，

2°假設n=k（k>1）時，結論成立，即bk=2k2，

則n=k+1時，ak=bk-k=2k2-k，，

ak+1=(2k+1)(k+1)，

∴bk+1=ak+1+(k+1)=(2k+1)(k+1)+(k+1)=2(k+1)2，

∴n=k+1時結論成立，

∴對所有正整數n，bn=2n2．

（3）由（2）知n2時，，

∴

，

．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

【題目】某校從高二年級學生中隨機抽取100名學生，將他們某次考試的數學成績（均為整數）分成六段：[40，50），[50，60），…，[90，100]后得到頻率分布直方圖（如圖所示），

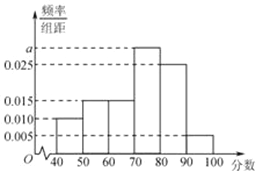
（1）求分數在[70，80）中的人數；

（2）若用分層抽樣的方法從分數在[40，50）和[50，60）的學生中共抽取5 人，該5 人中成績在[40，50）的有幾人？

（3）在（2）中抽取的5人中，隨機選取2 人，求分數在[40，50）和[50，60）各1 人的概率．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知拋物線過點，且焦點為F，直線l與拋物線相交于A，B兩點．

⑴求拋物線C的方程，并求其準線方程；

⑵為坐標原點.若，證明直線l必過一定點，并求出該定點．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】如圖，在四棱錐中， ，且．

（Ⅰ）當時，證明：平面平面；

（Ⅱ）當四棱錐的體積為，且二面角為鈍角時，求直線與平面所成角的正弦值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在△ABC中,邊a、b、c分別是角A、B、C的對邊,且滿足bcosC=(3a-c)cosB

(1)求cosB

(2)若△ABC的面積為4,b=4,求△ABC的周長

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】（本小題滿分12分）

已知拋物線C的方程C：y2="2" p x（p＞0）過點A（1，-2）.

（I）求拋物線C的方程，并求其準線方程；

（II）是否存在平行于OA（O為坐標原點）的直線l，使得直線l與拋物線C有公共點，且直線OA與l的距離等于？若存在，求出直線l的方程；若不存在，說明理由。

【答案】（I）拋物線C的方程為，其準線方程為（II）符合題意的直線l 存在，其方程為2x+y-1 =0.

【解析】

試題（Ⅰ）求拋物線標準方程，一般利用待定系數法，只需一個獨立條件確定p的值：（－2）2＝2p·1，所以p＝2．再由拋物線方程確定其準線方程：，（Ⅱ）由題意設：，先由直線OA與的距離等于根據兩條平行線距離公式得：解得，再根據直線與拋物線C有公共點確定

試題解析：解 （1）將（1，－2）代入y2＝2px，得（－2）2＝2p·1，

所以p＝2．

故所求的拋物線C的方程為

其準線方程為．

（2）假設存在符合題意的直線，

其方程為．

由得．

因為直線與拋物線C有公共點，

所以Δ＝4＋8t≥0，解得．

另一方面，由直線OA到的距離

可得，解得．

因為－1[－，＋∞），1∈[－，＋∞），

所以符合題意的直線存在，其方程為．

考點：拋物線方程，直線與拋物線位置關系

【名師點睛】求拋物線的標準方程的方法及流程

（1）方法：求拋物線的標準方程常用待定系數法，因為未知數只有p，所以只需一個條件確定p值即可．

（2）流程：因為拋物線方程有四種標準形式，因此求拋物線方程時，需先定位，再定量．

提醒：求標準方程要先確定形式，必要時要進行分類討論，標準方程有時可設為y2=mx或x2=my（m≠0）．

【題型】解答題
【結束】
22

【題目】已知橢圓：的左右焦點與其短軸的一個端點是正三角形的三個頂點，點在橢圓上.

（1）求橢圓的方程；

（2）直線過橢圓左焦點交橢圓于，為橢圓短軸的上頂點，當直線時，求的面積.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】在△ABC中，角A，B，C對應的邊分別是a，b，c，已知cos2A﹣3cos（B+C）=1．

（1）求角A的大小；

（2）若△ABC的面積S=5，b=5，求sinBsinC的值．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知函數.

（1）討論函數的單調性；

（2）若直線與曲線的交點的橫坐標為，且，求整數所有可能的值.

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】(2017·江蘇高考)如圖，在三棱錐ABCD中，AB⊥AD，BC⊥BD，平面ABD⊥平面BCD，點E，F(E與A，D不重合)分別在棱AD，BD上，且EF⊥AD.

求證：(1)EF∥平面ABC；

(2)AD⊥AC.

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 日韩精品一区二区三区在线播放 | 成人在线一区二区 | a免费在线观看 | 久久久大 | 久久久www成人免费精品 | 美女视频一区二区三区 | 欧美国产在线视频 | 久久久久成人精品 | 欧美a在线| 国产精品久久视频 | 久久久久久久久成人 | 黄色片视频在线观看 | 97国产精品 | 在线欧美视频 | 园产精品久久久久久久7电影 | 一本色道精品久久一区二区三区 | 国产高清视频一区二区 | 亚洲国产精品99久久久久久久久 | 忘忧草精品久久久久久久高清 | 成人妇女免费播放久久久 | 亚洲免费综合 | 中文字幕日本在线 | 亚洲精选免费视频 | 午夜激情影院 | 日本不卡免费新一二三区 | 久久久久一区 | 欧美精品成人 | 韩国毛片在线观看 | 一区二区三区回区在观看免费视频 | 欧美视频a| 在线不卡视频 | 黄色羞羞视频在线观看 | 日韩一区二区三区av | 久久av网| 在线99视频 | 亚洲福利一区 | 99精品国产热久久91蜜凸 | 作爱视频免费看 | 日本xxxxx片免费观看19 | 国产www在线 | 中文字幕精品一区 |