【題目】已知函數
.
（1）討論
的單調性；
（2）當
,
為兩個不相等的正數，證明：
.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知橢圓C：
過點A
，兩個焦點為（-1，0），（1，0）。
（Ⅰ）求橢圓C的方程；
（Ⅱ）E,F是橢圓C上的兩個動點，如果直線AE的斜率與AF的斜率互為相反數，證明直線EF的斜率為定值，并求出這個定值。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】人的正常體溫在
至
之間，下圖是一位病人在治療期間的體溫變化圖.
現有下述四個結論：
①此病人已明顯好轉；
②治療期間的體溫極差小于
；
③從每8小時的變化來看，25日0時~8時體溫最穩定；
④從3月22日8時開始，每8小時量一次體溫，若體溫不低于
就服用退燒藥，根據圖中信息可知該病人服用了3次退燒藥.
其中所有正確結論的編號是（ ）
A.③④B.②③C.①②④D.①②③
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）＝x2+2alnx.
(1)若函數f（x）的圖象在（2，f（2））處的切線斜率為1，求實數a的值；
(2)若函數
在[1，2]上是減函數，求實數a的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設無窮數列
的前
項和為
，已知
，
．
（1）求
的值；
（2）求數列的通項公式；
（3）是否存在數列
的一個無窮子數列
，使
對一切
均成立?若存在，請寫出數列的所有通項公式；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
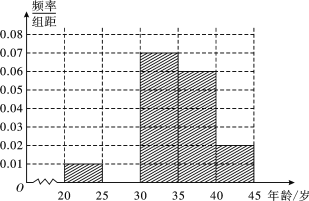
【題目】為增強市民交通規范意識,我市面向全市征召勸導員志愿者,分布于各候車亭或十字路口處．現從符合條件的500名志愿者中隨機抽取100名志愿者,他們的年齡情況如下表所示．
分組（單位：歲） | 頻數 | 頻率 |
| 5 |
|
| ① |
|
|
| ② |
|
|
|
|
|
|
合計 |
|
|
（1）頻率分布表中的①、②位置應填什么數據？并在答題卡中補全頻率分布直方圖（如圖）,再根據頻率分布直方圖估計這500名志愿者中年齡在[30,35)歲的人數；
（2）在抽出的100名志愿者中按年齡再采用分層抽樣法抽取20人參加“規范摩的司機的交通意識”培訓活動,從這20人中選取2名志愿者擔任主要負責人,記這2名志愿者中“年齡低于30歲”的人數為X,求X的分布列及數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，且滿足
；數列
的前項和為
，且滿足
，
，
．
（1）求數列的通項公式；
（2）求數列的通項公式；
（3）是否存在正整數，使得
恰為數列中的一項？若存在，求滿足要求的那幾項；若不存在，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某公司為了提高職工的健身意識，鼓勵大家加入健步運動，要求200名職工每天晚上9:30上傳手機計步截圖，對于步數超過10000的予以獎勵.圖1為甲乙兩名職工在某一星期內的運動步數統計圖，圖2為根據這星期內某一天全體職工的運動步數做出的頻率分布直方圖.
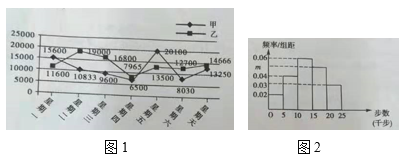
（1）在這一周內任選兩天檢查，求甲乙兩人兩天全部獲獎的概率；
（2）請根據頻率分布直方圖，求出該天運動步數不少于15000的人數，并估計全體職工在該天的平均步數；
（3）如果當天甲的排名為第130名，乙的排名為第40名，試判斷做出的是星期幾的頻率分布直方圖.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（a∈R，e為自然對數的底數），
，其中
在x=0處的切線方程為y=bx.
（1）求a，b的值；
（2）求證：
；
（3）求證：有且僅有兩個零點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
