
【題目】已知函數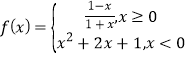 ,函數g(x)=f(1-x)-kx+k-
,函數g(x)=f(1-x)-kx+k-![]() 恰有三個不同的零點,則k的取值范圍是( )
恰有三個不同的零點,則k的取值范圍是( )
A. (-2-![]() ,0]∪
,0]∪![]() B. (-2+
B. (-2+![]() ,0]∪
,0]∪![]()
C. (-2-![]() ,0]∪
,0]∪![]() D. (-2+
D. (-2+![]() ,0]∪
,0]∪![]()
【答案】D
【解析】
g(x)=f(1-x)-kx+k-![]() 恰有三個不同的零點,即方程f(1-x)=k(x-1)+
恰有三個不同的零點,即方程f(1-x)=k(x-1)+![]() 恰有3個不同實根,令1-x=t,則方程f(t)=-kt+
恰有3個不同實根,令1-x=t,則方程f(t)=-kt+![]() 恰有三個不同實根,即函數y=f(x)與y=-kx+
恰有三個不同實根,即函數y=f(x)與y=-kx+![]() 的圖象恰有3個不同交點,數形結合即可求解.
的圖象恰有3個不同交點,數形結合即可求解.
∵g(x)=f(1-x)-kx+k-![]() 恰有3個不同零點,∴方程f(1-x)=k(x-1)+
恰有3個不同零點,∴方程f(1-x)=k(x-1)+![]() 恰有3個不同實根,令1-x=t,則方程f(t)=-kt+
恰有3個不同實根,令1-x=t,則方程f(t)=-kt+![]() 恰有三個不同實根,即函數y=f(x)與y=-kx+
恰有三個不同實根,即函數y=f(x)與y=-kx+![]() 的圖象恰有3個不同交點,畫出函數圖象如下圖:
的圖象恰有3個不同交點,畫出函數圖象如下圖:
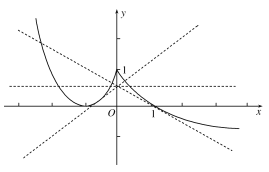
當-k=0即k=0時有三個交點,當y=-kx+![]() 與f(x)=x2+2x+1(x<0)相切時可求得k=-2+
與f(x)=x2+2x+1(x<0)相切時可求得k=-2+![]() ,當y=-kx+
,當y=-kx+![]() 與f(x)=
與f(x)=![]() ,x≥0相切時可求得k=
,x≥0相切時可求得k=![]() ,故由圖可得-2+
,故由圖可得-2+![]() <k≤0或k=
<k≤0或k=![]() 時函數y=f(x)與y=-kx+
時函數y=f(x)與y=-kx+![]() 的圖象恰有3個不同交點,即函數g(x)=f(1-x)-kx+k-
的圖象恰有3個不同交點,即函數g(x)=f(1-x)-kx+k-![]() 恰有3個不同零點,故選D.
恰有3個不同零點,故選D.


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案科目:高中數學 來源: 題型:
【題目】為支援邊遠地區教育事業的發展,現有5名師范大學畢業生主動要求赴西部某地區三所不同的學校去支教,每個學校至少去1人,甲、乙不能安排在同一所學校,則不同的安排方法有( )
A.180種B.150種C.90種D.114種
查看答案和解析>>
科目:高中數學 來源: 題型:
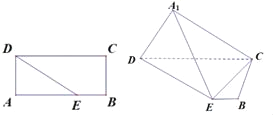
【題目】如圖(1)在矩形ABCD中,AB=5,AD=2,點E在線段AB上,且BE=1,將△ADE沿DE折起到△A1DE的位置,使得平面A1DE⊥平面BCDE,如圖(2).
(1)求證:CE⊥平面A1DE;
(2)求證:A1D⊥A1C;
(3)線段A1C上是否存在一點F,使得BF∥平面A1DE?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象與x軸交點為
的圖象與x軸交點為![]() ,與此交點距離最小的最高點坐標為
,與此交點距離最小的最高點坐標為![]() .
.
(Ⅰ)求函數![]() 的表達式;
的表達式;
(Ⅱ)若函數![]() 滿足方程
滿足方程![]() ,求方程在
,求方程在![]() 內的所有實數根之和;
內的所有實數根之和;
(Ⅲ)把函數![]() 的圖像的周期擴大為原來的兩倍,然后向右平移
的圖像的周期擴大為原來的兩倍,然后向右平移![]() 個單位,再把縱坐標伸長為原來的兩倍,最后向上平移一個單位得到函數
個單位,再把縱坐標伸長為原來的兩倍,最后向上平移一個單位得到函數![]() 的圖像.若對任意的
的圖像.若對任意的![]() ,方程
,方程![]() 在區間
在區間![]() 上至多有一個解,求正數k的取值范圍.
上至多有一個解,求正數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙兩人進行圍棋比賽,約定先連勝兩局者直接贏得比賽.若賽完5局仍未出現連勝,則判定獲勝局數多者贏得比賽.假設每局甲獲勝的概率為![]() ,乙獲勝的概率為
,乙獲勝的概率為![]() ,各局比賽結果相互獨立.
,各局比賽結果相互獨立.
(1)求甲在4局以內(含4局)贏得比賽的概率;
(2)記X為比賽決出勝負時的總局數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知非單調數列{an}是公比為q的等比數列,a1=![]() ,其前n項和為Sn(n∈N*),且滿足S3+a3,S5+a5,S4+a4成等差數列.
,其前n項和為Sn(n∈N*),且滿足S3+a3,S5+a5,S4+a4成等差數列.
(1)求數列{an}的通項公式和前n項和Sn;
(2)bn=![]() +
+![]() ,求數列{bn}的前n項和Tn.
,求數列{bn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,直角梯形公園![]() 中,
中,![]() ,
,![]() ,
,![]() ,公園的左下角陰影部分為以
,公園的左下角陰影部分為以![]() 為圓心,半徑為
為圓心,半徑為![]() 的
的![]() 圓面的人工湖,現設計修建一條與圓相切的觀光道路
圓面的人工湖,現設計修建一條與圓相切的觀光道路![]() (點
(點![]() 分別在
分別在![]() 與
與![]() 上),
上),![]() 為切點,設
為切點,設![]() .
.

(1)試求觀光道路![]() 長度的最大值;
長度的最大值;
(2)公園計劃在道路![]() 的右側種植草坪,試求草坪
的右側種植草坪,試求草坪![]() 的面積最大值.
的面積最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com