
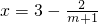 ,已知今年生產的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).(I)將今年該產品的利潤y(萬元)表示為年促銷費m(萬元)的函數;(II)求今年該產品利潤的最大值,此時年促銷費為多少萬元?
,已知今年生產的固定投入為8萬元,每生產1萬件該產品需要再投入16萬元,廠家將每件產品的銷售價格定為每件產品平均成本的1.5倍(產品成本包括固定投入和再投入兩部分資金).(I)將今年該產品的利潤y(萬元)表示為年促銷費m(萬元)的函數;(II)求今年該產品利潤的最大值,此時年促銷費為多少萬元?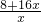 元,且x=
元,且x=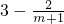 ,則
,則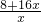 •x-(8+16x+m)=4+8x-m=4+8
•x-(8+16x+m)=4+8x-m=4+8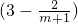 -m=28-
-m=28- -m(其中m≥0),
-m(其中m≥0), m≥0;
m≥0; =29-[
=29-[ +m+1]≤29-2
+m+1]≤29-2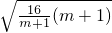 =21,
=21, =m+1(其中m≥0),即m=3(萬元)時,等號成立;
=m+1(其中m≥0),即m=3(萬元)時,等號成立;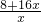 元,且x=
元,且x=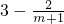 ,則利潤函數y=1.5×
,則利潤函數y=1.5×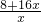 •x-(8+16x+m),整理即可;
•x-(8+16x+m),整理即可; ,構造條件應用基本不等式,可求得函數y的最大值及對應的m值.
,構造條件應用基本不等式,可求得函數y的最大值及對應的m值. (a>0,b>0)求函數的最值問題,是中檔題.
(a>0,b>0)求函數的最值問題,是中檔題. 

 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com