
(1)a2sin(-1 350°)+b2tan405°-(a-b)2cot765°-2abcos(-1 080°);
(2)sin(-![]() )+cos
)+cos![]() ·tan4π-
·tan4π-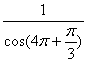 .
.
解析:(1)原式=a2sin(-4×360°+90°)+b2tan(360°+45°)-(a-b)2·cot(2×360°+45°)-2abcos(-3×360°)
=a2sin90°+b2tan45°-(a-b)2cot45°-2abcos0°
=a2+b2-(a-b)2-2ab=0.
(2)原式=sin(-2π+![]() )+cos
)+cos![]() ·tan0-
·tan0-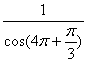 =sin
=sin![]() +0-
+0-![]() =
=![]() -2=-
-2=-![]() .
.
點評:公式一有兩個作用:其一,可以把任意角的正弦、余弦、正切函數值分別化為0到2π(或0°到360°)角的同一三角函數值(其方法是先在[0,2π)范圍內找出與它終邊相同的角,再把它寫成公式一的形式,然后得出結果);其二,便于研究這三種三角函數的性質.


科目:高中數學 來源: 題型:
(1)cos(80°+3α)cos(35°+3α)+sin(80°+3α)cos(55°-3α);
(2)sin(x+![]() )+2sin(x-
)+2sin(x-![]() )-
)-![]() cos(
cos(![]() -x);
-x);
(3)![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com