
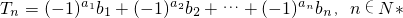 .證明|Tn|<2n2,n≥3.
.證明|Tn|<2n2,n≥3. ,bn=(n+1)2,n∈N*.
,bn=(n+1)2,n∈N*. ,n∈N*.
,n∈N*.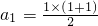 ,等式成立.當n≥2時用數學歸納法證明如下:
,等式成立.當n≥2時用數學歸納法證明如下: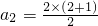 ,等式成立.
,等式成立. ,k≥2.
,k≥2.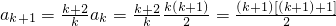 .
. 對任何的n≥2成立.
對任何的n≥2成立. 對任何的n∈N*都成立
對任何的n∈N*都成立
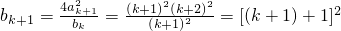 .
.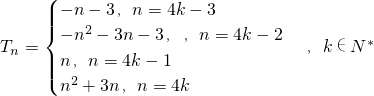 .
.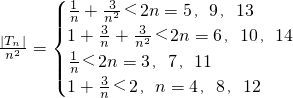
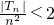 ,即|Tn|<2n2.
,即|Tn|<2n2. ,bn=(n+1)2,n∈N*.再用數學歸納法進行證明.
,bn=(n+1)2,n∈N*.再用數學歸納法進行證明.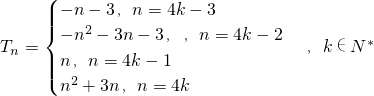 .由此可以導出|Tn|<2n2.
.由此可以導出|Tn|<2n2.

 一線名師提優試卷系列答案
一線名師提優試卷系列答案科目:高中數學 來源: 題型:
| A、某校高三1班有55人,2班有54人,3班有52人,由此得高三所有班人數超過50人 | ||||
| B、兩條直線平行,同旁內角互補,如果∠A與∠B是兩條平行直線的同旁內角,則∠A+∠B=180° | ||||
| C、由平面三角形的性質,推測空間四面體性質 | ||||
D、在數列{an}中a1=1,an=
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、兩條直線平行,同旁內角互補,如果∠A與∠B是兩條平行直線的同旁內角,則∠A+∠B=180° | ||||
| B、某校高二(1)班有55人,高二(2)班有52人,由此得高二所有班人數超過50人 | ||||
| C、由平面三角形的性質,推出空間四邊形的性質 | ||||
D、在數列{an}中,a1=1,an=
|
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com