Question

已知f(x)是定義在[－1，1]上的奇函數，且f(1)＝1，若a，b∈[－1，1]，a＋b≠0有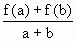＞0恒成立．

(Ⅰ)判斷f(x)在[－1，1]上是增函數還是減函數，并證明你的結論；

(Ⅱ)解不等式f(x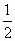＋)＜f()；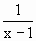

(Ⅲ)若f(x)≤m²－2am＋1，對所有x∈[－1，1]，a∈[－1，1]恒成立，求實數m的取值范圍．

Answer 1

答案：
解析：

解(Ⅰ)設x1＜x2且x1，x2∈[－1，1]，則－x2∈[－1，1]　　∵f(x)是奇函數 　　∴f(x1)－f(x2)＝f(x1)＋f(－x2)＝(x1－x2) 　　由題設知＞0且x1－x2＜0 　　∴(x1－x2)＜0，即f(x1)－f(x2)＜0　　∴f(x1)＜f(x2) 　　∴f(x)在[－1，1]上是增函數 　　(Ⅱ)∵f(x)在[－1，1]上是增函數，不等式等價于 　　 　　∴－≤x＜－1 　　(Ⅲ)解法一：由(Ⅰ)知，f(x)在[－1，1]上是增函數，且f(1)＝1 　　∴|f(x)|≤f(1)＝1 　　要f(x)≤m2－2am＋1，對所有x∈[－1，1]，a∈[－1，1]恒成立 　　必f(x)max＝1≤m2－2am＋1成立　　∴必m2－2am≥0 　　令g(a)＝－2am＋m2，對a∈[－1，1]，g(a)≥0恒成立 　　只要g(a)最小值大于或等于0 　　(i)當m＜0時，g(a)是增函數，必g(－1)＝2m＋m2≥0 　　∴m≤－2或m≥0，由m＜0　　∴m≤－2 　　(ii)當m＝0時，g(a)＝0恒成立 　　(iii)當m＞0時，g(a)在[－1，1]上是減函數，必g(1)＝－2m＋m2≥0 　　∴m≤0或m≥2，∵m＞0，∴m≥2 　　綜上知，m≤－2或m＝0或m≥2 　　解法二：令g(a)＝－2am＋m2，對a∈[－1，1]，g(a)≥0恒成立 　　只要g(a)滿足 　　∴m≤－2或m＝0或m≥2