【題目】已知函數
在區間
上的最大值為2.
(1)求函數
的解析式，并求它的對稱中心的坐標；
(2)先將函數保持橫坐標不變，縱坐標變為原來的
（
）倍，再將圖象向左平移
（
）個單位，得到的函數
為偶函數．若對任意的
，總存在
，使得
成立，求實數
的取值范圍.
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目：高中數學 來源： 題型：
【題目】已知點
為圓
的圓心， 
是圓上的動點，點
在圓的半徑
上，且有點
和
上的點
，滿足
， 
.
（1）當點
在圓上運動時，求點
的軌跡方程；
（2）若斜率為
的直線
與圓
相切，直線
與（1）中所求點
的軌跡交于不同的兩點
， 
， 
是坐標原點，且
時，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的左頂點，右焦點分別為
，右準線為
，
（1）若直線上不存在點
，使
為等腰三角形，求橢圓離心率的取值范圍；
（2）在（1）的條件下，當
取最大值時，
點坐標為
，設
是橢圓上的三點，且
，求：以線段
的中心為原點，過兩點的圓方程.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，已知點
到拋物線
焦點的距離為
．
（1）求
的值；
（2） 設
是拋物線上異于
的兩個不同點，過
作
軸的垂線，與直線
交于點
，過
作軸的垂線，與直線
交于點
，過作軸的垂線，與直線
分別交于點
．
求證：①直線
的斜率為定值；
②是線段
的中點．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解本屆高二學生對文理科的選擇與性別是否有關，現隨機從高二的全體學生中抽取了若干名學生，據統計，男生35人，理科生40人，理科男生30人，文科女生15人。
(1)完成如下2×2列聯表，判斷是否有99.9%的把握認為本屆高二學生“對文理科的選擇與性別有關”？
男生 | 女生 | 合計 | |
文科 | |||
理科 | |||
合計 |
(2)已采用分層抽樣的方式從樣本的所有女生中抽取了5人，現從這5人中隨機抽取2人參加座談會，求抽到的2人恰好一文一理的概率。
| 0.15 | 0.10 | 0.05 | 0.01 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
（參考公式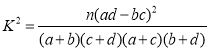
，其中
為樣本容量）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，長方體ABCD﹣A′B′C′D′中，AB=2 
，AD=2 ，AA′=2，
（Ⅰ）求異面直線BC′ 和AD所成的角；
（Ⅱ）求證：直線BC′∥平面ADD′A′．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，直線
的參數方程為
（
為參數），在極坐標系（與直角坐標系
取相同的長度單位，且以原點
為極點，以
軸正半軸為極軸）中，圓
的方程為
.
（1）求圓
的直角坐標方程；
（2）設圓
與直線
交于點
，若點
的坐標為
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2018·日照一模)如圖所示，ABCD－A1B1C1D1是長方體，O是B1D1的中點，直線A1C交平面AB1D1于點M，給出下列結論：
①A、M、O三點共線；②A、M、O、A1不共面；③A、M、C、O共面；④B、B1、O、M共面．
其中正確結論的序號為________．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
