
【題目】考拉茲猜想又名3n+1猜想,是指對于每一個正整數,如果它是奇數,則對它乘3再加1;如果它是偶數,則對它除以2.如此循環,最終都能得到1.閱讀如圖所示的程序框圖,運行相應程序,輸出的結果i=( ) 
A.4
B.5
C.6
D.7
科目:高中數學 來源: 題型:
【題目】已知f(x)=aln(x2+1)+bx存在兩個極值點x1 , x2 .
(1)求證:|x1+x2|>2;
(2)若實數λ滿足等式f(x1)+f(x2)+a+λb=0,試求λ的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 與
與![]() 軸,
軸,![]() 軸的正半軸分別交于A,B兩點,原點O到直線AB的距離為
軸的正半軸分別交于A,B兩點,原點O到直線AB的距離為![]() 該橢圓的離心率為
該橢圓的離心率為![]()
(1)求橢圓的方程
(2)是否存在過點P(![]() 的直線
的直線![]() 與橢圓交于M,N兩個不同的點,使
與橢圓交于M,N兩個不同的點,使![]() 成立?若存在,求出
成立?若存在,求出![]() 的方程;若不存在,說明理由。
的方程;若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下圖是某市3月1日至14日的空氣質量指數趨勢圖,空氣質量指數小于100表示空氣質量優良,空氣質量指數大于200表示空氣重度污染,某人隨機選擇3月1日至3月15日中的某一天到達該市,并停留2天.
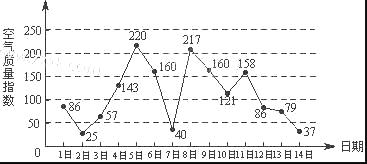
(Ⅰ)求此人到達當日空氣質量優良的概率;
(Ⅱ)求此人在該市停留期間只有1天空氣重度污染的概率;
(Ⅲ)由圖判斷從哪天開始連續三天的空氣質量指數方差最大?(結論不要求證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx+bx﹣c,f(x)在點(1,f(1))處的切線方程為x+y+4=0.
(1)求f(x)的解析式;
(2)求f(x)的單調區間;
(3)若在區間 ![]() 內,恒有f(x)≥2lnx+kx成立,求k的取值范圍.
內,恒有f(x)≥2lnx+kx成立,求k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,A1 , B1分別是邊BA,CB的中點,A2 , B2分別是線段A1A,B1B的中點,…,An , Bn分別是線段 ![]() 的中點,設數列{an},{bn}滿足:向量
的中點,設數列{an},{bn}滿足:向量 ![]() ,有下列四個命題,其中假命題是( )
,有下列四個命題,其中假命題是( )
A.數列{an}是單調遞增數列,數列{bn}是單調遞減數列
B.數列{an+bn}是等比數列
C.數列 ![]() 有最小值,無最大值
有最小值,無最大值
D.若△ABC中,C=90°,CA=CB,則 ![]() 最小時,
最小時, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等差數列{an}.滿足:an+1>an(n∈N*),a1=1,該數列的前三項分別加上1,1,3后成等比數列,an+2log2bn=﹣1.
(Ⅰ)分別求數列{an},{bn}的通項公式;
(Ⅱ)求數列{anbn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C過點![]() ,且與圓
,且與圓![]() 外切于點
外切于點![]() ,
,![]() 是x軸上的一個動點.
是x軸上的一個動點.
![]() 求圓C的標準方程;
求圓C的標準方程;
![]() 當圓C上存在點Q,使
當圓C上存在點Q,使![]() ,求實數m的取值范圍;
,求實數m的取值范圍;
![]() 當
當![]() 時,過P作直線PA,PB與圓C分別交于異于點P的點A,B兩點,且
時,過P作直線PA,PB與圓C分別交于異于點P的點A,B兩點,且![]() 求證:直線AB恒過定點.
求證:直線AB恒過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com