
【題目】已知f(x)=sinx﹣cosx,x∈[0,+∞).
(1)證明: ![]() ;
;
(2)證明:當a≥1時,f(x)≤eax﹣2.
【答案】
(1)解:不等式 ![]() ,即不等式
,即不等式 ![]() ,
,
設 ![]() ,則g'(x)=﹣sinx+x,x∈[0,+∞),
,則g'(x)=﹣sinx+x,x∈[0,+∞),
再次構造函數h(x)=﹣sinx+x,則h'(x)=﹣cosx+1≥0在x∈[0,+∞)時恒成立,
所以函數h(x)在[0,+∞)上單調遞增,
所以h(x)≥h(0)=0,
所以g'(x)≥0在[0,+∞)上恒成立,
所以函數g(x)在[0,+∞)上單調遞增,
所以g(x)≥g(0)=0,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() 成立
成立
(2)解:由(1)的解析可知,當x∈[0,+∞)時,sinx≤x且 ![]() ,
,
所以 ![]() ,
,
當 ![]() 對x∈[0,+∞)恒成立時,不等式f(x)≤eax﹣2恒成立,
對x∈[0,+∞)恒成立時,不等式f(x)≤eax﹣2恒成立,
不等式 ![]() ,即不等式
,即不等式 ![]() ,對x∈[0,+∞)恒成立,
,對x∈[0,+∞)恒成立,
構造函數 ![]() ,
,
則M'(x)=ex﹣x﹣1,
令m(x)=ex﹣x﹣1,
則m'(x)=ex﹣1,當x∈[0,+∞)時,m'(x)≥0,
故m(x)在[0,+∞)上單調遞增,
所以m(x)≥m(0)=0,故M'(x)≥0,即M(x)在[0,+∞)上單調遞增,
所以M(x)≥M(0)=0,
故 ![]() 恒成立,
恒成立,
故當a≥1時, ![]() ,
,
即當a≥1時,不等式f(x)≤eax﹣2恒成立
【解析】(1)設 ![]() ,則g'(x)=﹣sinx+x,x∈[0,+∞),再次構造函數h(x)=﹣sinx+x,則h'(x)=﹣cosx+1≥0在x∈[0,+∞)時恒成立,可得g'(x)≥0在[0,+∞)上恒成立,可得
,則g'(x)=﹣sinx+x,x∈[0,+∞),再次構造函數h(x)=﹣sinx+x,則h'(x)=﹣cosx+1≥0在x∈[0,+∞)時恒成立,可得g'(x)≥0在[0,+∞)上恒成立,可得 ![]() ,即可得證.(2)由(1)可知,不等式
,即可得證.(2)由(1)可知,不等式 ![]() ,對x∈[0,+∞)恒成立,構造函數
,對x∈[0,+∞)恒成立,構造函數 ![]() ,令m(x)=ex﹣x﹣1,則m'(x)=ex﹣1,當x∈[0,+∞)時,m'(x)≥0,可得
,令m(x)=ex﹣x﹣1,則m'(x)=ex﹣1,當x∈[0,+∞)時,m'(x)≥0,可得 ![]() 恒成立,從而得證,當a≥1時,不等式f(x)≤eax﹣2恒成立.
恒成立,從而得證,當a≥1時,不等式f(x)≤eax﹣2恒成立.


科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x)為偶函數,且滿足f(x)=f(x+2),f(﹣1)=1,若數列{an}的前n項和Sn滿足2Sn=an+1 , a1= ![]() ,則f(a5)+f(a6)=( )
,則f(a5)+f(a6)=( )
A.4
B.2
C.1
D.0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為做好2022年北京冬季奧運會的宣傳工作,組委會計劃從某大學選取若干大學生志愿者,某記者在該大學隨機調查了1000名大學生,以了解他們是否愿意做志愿者工作,得到的數據如表所示:
愿意做志愿者工作 | 不愿意做志愿者工作 | 合計 | |
男大學生 | 610 | ||
女大學生 | 90 | ||
合計 | 800 |
(1)根據題意完成表格;
(2)是否有![]() 的把握認為愿意做志愿者工作與性別有關?
的把握認為愿意做志愿者工作與性別有關?
查看答案和解析>>
科目:高中數學 來源: 題型:
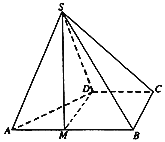
【題目】四棱錐S-ABCD的底面ABCD為直角梯形,AB∥CD,AB⊥BC,AB=2BC=2CD=2,△SAD為正三角形.
(Ⅰ)點M為棱AB上一點,若BC∥平面SDM,AM=λAB,求實數λ的值;
(Ⅱ)若BC⊥SD,求二面角A-SB-C的余弦值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(Ⅰ)由線面平行的性質定理可得![]() ,據此可知四邊形BCDM為平行四邊形,據此可得
,據此可知四邊形BCDM為平行四邊形,據此可得![]() .
.
(Ⅱ)由幾何關系,在平面![]() 內過點
內過點![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,以點E為坐標原點,EA方向為X軸,EC方向為Y軸,ES方向為Z軸建立空間坐標系,據此可得平面
,以點E為坐標原點,EA方向為X軸,EC方向為Y軸,ES方向為Z軸建立空間坐標系,據此可得平面![]() 的一個法向量
的一個法向量![]() ,平面
,平面![]() 的一個法向量
的一個法向量![]() ,據此計算可得二面角
,據此計算可得二面角![]() 余弦值為
余弦值為![]() .
.
(Ⅰ)因為![]() 平面SDM,
平面SDM,![]()
![]() 平面ABCD,平面SDM
平面ABCD,平面SDM ![]() 平面ABCD=DM,所以
平面ABCD=DM,所以![]() ,
,
因為![]() ,所以四邊形BCDM為平行四邊形,又
,所以四邊形BCDM為平行四邊形,又![]() ,所以M為AB的中點.
,所以M為AB的中點.
因為![]()
![]() .
.

(Ⅱ)因為![]()
![]() ,
, ![]()
![]() ,所以
,所以![]() 平面
平面![]() ,又因為
,又因為![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
在平面![]() 內過點
內過點![]() 作
作![]() 直線
直線![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,
,
在![]() 和
和![]() 中,因為
中,因為![]() ,所以
,所以![]() ,
,
又由題知![]() ,所以
,所以![]() 所以
所以![]() ,
,
以下建系求解.以點E為坐標原點,EA方向為X軸,EC方向為Y軸,ES方向為Z軸建立如圖所示空間坐標系,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量
的法向量![]() ,則
,則 ,所
,所![]() ,
,
令![]() 得
得![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
同理得![]() 為平面
為平面![]() 的一個法向量,
的一個法向量,
 ,因為二面角
,因為二面角![]() 為鈍角.
為鈍角.
所以二面角![]() 余弦值為
余弦值為![]() .
.
【點睛】
本題考查了立體幾何中的判斷定理和二面角的求解問題,意在考查學生的空間想象能力和邏輯推理能力;解答本題關鍵在于能利用直線與直線、直線與平面、平面與平面關系的相互轉化,通過嚴密推理,明確角的構成.同時對于立體幾何中角的計算問題,往往可以利用空間向量法,通過求解平面的法向量,利用向量的夾角公式求解.
【題型】解答題
【結束】
19
【題目】小明在石家莊市某物流派送公司找到了一份派送員的工作,該公司給出了兩種日薪薪酬方案.甲方案:底薪100元,每派送一單獎勵1元;乙方案:底薪140元,每日前55單沒有獎勵,超過55單的部分每單獎勵12元.
(Ⅰ)請分別求出甲、乙兩種薪酬方案中日薪y(單位:元)與送貨單數n的函數關系式;
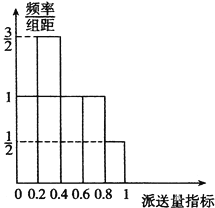
(Ⅱ)根據該公司所有派送員100天的派送記錄,發現派送員的日平均派送單數滿足以下條件:在這100天中的派送量指標滿足如圖所示的直方圖,其中當某天的派送量指標在(![]() ,
,![]() ](n=1,2,3,4,5)時,日平均派送量為50+2n單.若將頻率視為概率,回答下列問題:
](n=1,2,3,4,5)時,日平均派送量為50+2n單.若將頻率視為概率,回答下列問題:
①根據以上數據,設每名派送員的日薪為X(單位:元),試分別求出甲、乙兩種方案的日薪X的分布列,數學期望及方差;
②結合①中的數據,根據統計學的思想,幫助小明分析,他選擇哪種薪酬方案比較合適,并說明你的理由。
(參考數據:0.62=0.36,1.42=1.9 6,2.6 2=6.76,3.42=1 1.56,3.62=12.96,4.62=21.16,15.62=243.36,20.42=416.16,44.42=1971.36)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣ax,a>0.
(1)記f(x)的極小值為g(a),求g(a)的最大值;
(2)若對任意實數x恒有f(x)≥0,求f(a)的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某路段最高限速60km/h,電子監控測得連續6輛汽車的速度用莖葉圖表示如下(單位:km/h).若從中任取2輛,則恰好有1輛汽車超速的概率為( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下表是某廠生產某種產品的過程中記錄的幾組數據,其中![]() 表示產量(單位:噸),
表示產量(單位:噸),![]() 表示生產中消耗的煤的數量(單位:噸).
表示生產中消耗的煤的數量(單位:噸).
|
|
|
|
|
|
|
|
|
|
|
|
(1)試在給出的坐標系下作出散點圖,根據散點圖判斷,在![]() 與
與![]() 中,哪一個方程更適合作為變量
中,哪一個方程更適合作為變量![]() 關于
關于![]() 的回歸方程模型?(給出判斷即可,不需要說明理由)
的回歸方程模型?(給出判斷即可,不需要說明理由)
(2)根據(1)的結果以及表中數據,建立變量![]() 關于
關于![]() 的回歸方程.并估計生產
的回歸方程.并估計生產![]() 噸產品需要準備多少噸煤.參考公式:
噸產品需要準備多少噸煤.參考公式: .
.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x﹣a|+|x+2|.
(1)當a=1 時,求不等式f(x)≤5的解集;
(2)x0∈R,f(x0)≤|2a+1|,求a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com