
【題目】環境監測中心監測我市空氣質量,每天都要記錄空氣質量指數(指數采取10分制,保留一位小數).現隨機抽取20天的指數(見下表),將指數不低于8.5視為當天空氣質量優良.
天數 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
空氣質量指數 | 7.1 | 8.3 | 7.3 | 9.5 | 8.6 | 7.7 | 8.7 | 8.8 | 8.7 | 9.1 |
天數 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
空氣質量指數 | 7.4 | 8.5 | 9.7 | 8.4 | 9.6 | 7.6 | 9.4 | 8.9 | 8.3 | 9.3 |
(Ⅰ)求從這20天隨機抽取3天,至少有2天空氣質量為優良的概率;
(Ⅱ)以這20天的數據估計我市總體空氣質量(天數很多).若從我市總體空氣質量指數中隨機抽取3天的指數,用X表示抽到空氣質量為優良的天數,求X的分布列及數學期望.
 優等生題庫系列答案
優等生題庫系列答案科目:高中數學 來源: 題型:
【題目】某縣農民年均收入服從μ=500元,σ=20元的正態分布,求:
(1)此縣農民的年均收入在500~520元之間的人數的百分比;
(2)此縣農民的年均收入超過540元的人數的百分比.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a<﹣1,函數f(x)=|x3﹣1|+x3+ax(x∈R).
(Ⅰ)求函數f(x)的最小值;
(Ⅱ)已知存在實數m,n(m<n≤1),對任意t0∈(m,n),總存在兩個不同的t1 , t2∈(1,+∞),
使得f(t0)﹣2=f(t1)=f(t2),求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體ABCD-A1B1C1D1中,如圖.
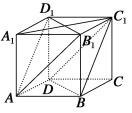
(1)求證:平面AB1D1∥平面C1BD;
(2)試找出體對角線A1C與平面AB1D1和平面C1BD的交點E,F,并證明:A1E=EF=FC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有某批次同一型號的產品共10件,其中有8件合格品,2件次品.
(Ⅰ)某檢驗員從中有放回地連續抽取產品2次,每次隨機抽取1件,求兩次都取到次品的概率;
(Ⅱ)若該檢驗員從中任意抽取2件,用X表示取出的2件產品中次品的件數,求X的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() (
(![]() ,
, ![]() )的圖象關于直線
)的圖象關于直線![]() 對稱,且圖像上相鄰兩個最高點的距離為
對稱,且圖像上相鄰兩個最高點的距離為![]() .
.
(1)求函數![]() 的解析式以及它的單調遞增區間;
的解析式以及它的單調遞增區間;
(2)是否存在實數![]() ,滿足不等式
,滿足不等式 ?若存在,求出
?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f′(x)是奇函數f(x)(x∈R)的導函數,f(﹣1)=0,當x>0時,xf′(x)﹣f(x)<0,則使得f(x)>0成立的x的取值范圍是( )
A.(﹣∞,﹣1)∪(0,1)
B.(﹣1,0)∪(1,+∞)
C.(﹣∞,﹣1)∪(﹣1,0)
D.(0,1)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在四棱錐P-ABCD中,底面是邊長為a的正方形,側棱PD=a,PA=PC=![]() a,
a,
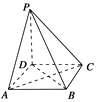
(1)求證:PD⊥平面ABCD;
(2)求證:平面PAC⊥平面PBD;
(3)求二面角P-AC-D的正切值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex﹣ax2﹣bx﹣1,其中a,b∈R,e=2.718 28…為自然對數的底數.
(1)設g(x)是函數f(x)的導函數,求函數g(x)在區間[0,1]上的最小值;
(2)若f(1)=0,函數f(x)在區間(0,1)內有零點,證明:e﹣2<a<1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com