Question

已知a∈R，討論函數f（x）=e^x（x²+ax+a+1）的極值點的個數．

Answer 1

【答案】分析：先求出f′（x）=0時得到方程討論△的取值決定方程解得個數從而得到函數極值的個數．
解答：解：f′（x）=e^x（x²+ax+a+1）+e^x（2x+a）
=e^x[x²+（a+2）x+（2a+1）]，
令f′（x）=0得x²+（a+2）x+（2a+1）=0
（1）當△=（a+2）²-4（2a+1）=a²-4a=a（a-4）＞0．
即a＜0或a＞4時，方程x²+（a+2）x+（2a+1）=0有兩個不同的實根x₁，x₂，不妨設x₁＜x₂，
于是f′（x）=e^x（x-x₁）（x-x₂），從而有下表：

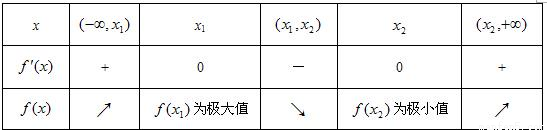
即此時f（x）有兩個極值點．
（2）當△=0即a=0或a=4時，方程x²+（a+2）x+（2a+1）=0有兩個相同的實根x₁=x₂
于是f'（x）=e^x（x-x₁）²故當x＜x₁時，f'（x）＞0；當x＞x₂時，f'（x）＞0，因此f（x）無極值．
（3）當△＜0，即0＜a＜4時，x²+（a+2）x+（2a+1）＞0，f'（x）=e^x[x²+（a+2）x+（2a+1）]＞0，故f（x）為增函數，此時f（x）無極值．因此當a＞4或a＜0時，f（x）有2個極值點，當0≤a≤4時，f（x）無極值點．
綜上所述：當a＜0或a＞4時，f（x）有兩個極值點．
點評：考查學生利用導數研究函數極值的能力，利用導數研究函數單調性的能力．