
| 1 |
| 4 |
 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源:2013屆黑龍江省大慶鐵人中學高三第三次階段理科數學試卷(帶解析) 題型:填空題
下列四個命題:
①直線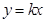 與圓
與圓 恒有公共點;
恒有公共點;
②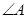 為△ABC的內角,則
為△ABC的內角,則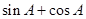 最小值為
最小值為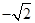 ;
;
③已知a,b是兩條異面直線,則過空間任意一點P都能作并且只能作一條直線與a,b都垂直;
④等差數列{ }中,
}中,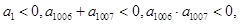 則使其前n項和
則使其前n項和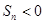 成立的最大正整數為2013;
成立的最大正整數為2013;
其中正確命題的序號為 。(將你認為正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源:2013屆山西省太原市第五中學高三4月月考文科數學試卷(帶解析) 題型:填空題
下列四個命題:
①直線 與圓
與圓 恒有公共點;
恒有公共點;
② 為△ABC的內角,則
為△ABC的內角,則 最小值為
最小值為 ;
;
③已知a,b是兩條異面直線,則過空間任意一點P都能作并且只能作一條直線與a,b都垂直;
④等差數列{ }中,
}中, 則使其前n項和
則使其前n項和 成立的最大正整數為2013;
成立的最大正整數為2013;
其中正確命題的序號為 。(將你認為正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源:2012-2013學年山西省太原市高三4月月考文科數學試卷(解析版) 題型:填空題
下列四個命題:
①直線 與圓
與圓 恒有公共點;
恒有公共點;
② 為△ABC的內角,則
為△ABC的內角,則 最小值為
最小值為 ;
;
③已知a,b是兩條異面直線,則過空間任意一點P都能作并且只能作一條直線與a,b都垂直;
④等差數列{ }中,
}中, 則使其前n項和
則使其前n項和 成立的最大正整數為2013;
成立的最大正整數為2013;
其中正確命題的序號為 。(將你認為正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源:2012-2013學年黑龍江省高三第三次階段理科數學試卷(解析版) 題型:填空題
下列四個命題:
①直線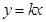 與圓
與圓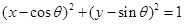 恒有公共點;
恒有公共點;
②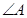 為△ABC的內角,則
為△ABC的內角,則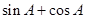 最小值為
最小值為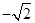 ;
;
③已知a,b是兩條異面直線,則過空間任意一點P都能作并且只能作一條直線與a,b都垂直;
④等差數列{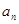 }中,
}中,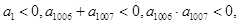 則使其前n項和
則使其前n項和 成立的最大正整數為2013;
成立的最大正整數為2013;
其中正確命題的序號為 。(將你認為正確的命題的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
(1)在AB上求一點D,使沿折線PDAO修建公路的總造價最小;
(2)對于(1)中得到的點D,在DA上求一點E,使沿折線PDEO修建公路的總造價最小;
(3)在AB上是否存在兩個不同的點D′,E′,使沿折線.PD′E′O修建公路的總造價小于(2)中得到的最小總造價?證明你的結論.

a)
第19題圖
(文)如圖b所示,直四棱柱ABCD-A1B1C1D1中,∠ADC=90°,△ABC為等邊三角形,且AA1=AD=DC=2.
(1)求AC1與BC所成角的余弦值;
(2)求二面角C1-BD-C的大小;
(3)設M是BD上的點,當DM為何值時,D1M⊥平面A1C1D?并證明你的結論.

第19題圖
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com