
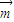 =(1,1),向量
=(1,1),向量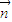 和向量
和向量 的夾角為
的夾角為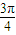 ,|
,|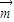 |=
|=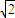 ,
,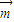 •
•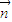 =-1.
=-1.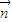 ;
;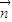 與向量
與向量 =(1,0)的夾角為
=(1,0)的夾角為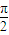 ,向量
,向量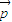 =(cosA,
=(cosA,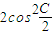 ),其中A、B、C為△ABC的內角a、b、c為三邊,b2+ac=a2+c2,求|
),其中A、B、C為△ABC的內角a、b、c為三邊,b2+ac=a2+c2,求| +
+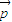 |的取值范圍.
|的取值范圍.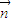
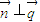 確定出
確定出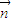 ,利用三角形的余弦定理求出∠B,利用向量模的坐標公式求出
,利用三角形的余弦定理求出∠B,利用向量模的坐標公式求出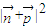 ,利用三角函數的二倍角公式化簡三角函數,利用整體思想求出三角函數的取值范圍.
,利用三角函數的二倍角公式化簡三角函數,利用整體思想求出三角函數的取值范圍.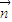 =(x,y),由
=(x,y),由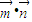 =-1得x+y=-1,
=-1得x+y=-1,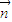 和
和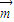 的夾角為
的夾角為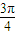 ,,
,,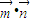 =
=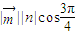 =-1,
=-1,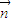 |=1⇒x2+y2=1,
|=1⇒x2+y2=1,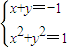 ,可解得
,可解得 =(-1,0)或(0,-1).
=(-1,0)或(0,-1).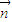 與
與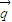 =(1,0)的夾角為
=(1,0)的夾角為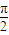 知
知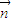 =(0,-1),
=(0,-1),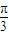 得∠A+∠C=
得∠A+∠C=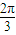 ,
,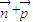 |2=
|2=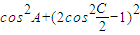 =cos2A+cos2C=
=cos2A+cos2C=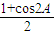 +
+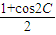

 =
=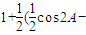
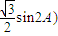 =1+
=1+
 .
.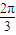 ⇒
⇒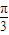 <
<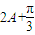 <
<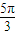 ⇒
⇒ ≤1+
≤1+
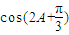 <
< ,
,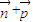 |的取值范圍為[
|的取值范圍為[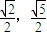 ).
).

科目:高中數學 來源: 題型:
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| 2 |
| m |
| n |
| n |
| n |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| n |
| p |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| b |
| n2+1 |
| a |
| b |
| lim |
| n→∞ |
查看答案和解析>>
科目:高中數學 來源:2012年蘇教版高中數學必修4 2.5向量的應用練習卷(解析版) 題型:填空題
(2008海南、寧夏高考,理13)已知向量 =(0,-1,1),
=(0,-1,1),  =(4,1,0),|λ
=(4,1,0),|λ +
+ |=
|=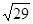 ,且λ>0,則λ=________________.
,且λ>0,則λ=________________.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| m |
| n |
| m |
| 3π |
| 4 |
| m |
| 2 |
| m |
| n |
| n |
| n |
| q |
| π |
| 2 |
| p |
| C |
| 2 |
| n |
| p |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com