
(本題滿分12分)、若函數y=f(x)是周期為2的偶函數,當x∈[2,3]時,f(x)=x-1.在y=f(x)的圖象上有兩點A、B,它們的縱坐標相等,橫坐標都在區間[1,3]上,
(1) 求當x∈[1,2]時,f(x)的解析式;
(2) 定點C的坐標為(0,a)(其中2<a<3),求△ABC面積的最大值.
(1)當x∈[1,2]時,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)當t=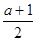 時,S最大值=
時,S最大值=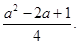
【解析】本試題主要是考查了函數的奇偶性和函數的解析式以及函數的最值的綜合運用。
(1)因為∵f(x)是以2為周期的周期函數,當x∈[2,3]時,f(x)=x-1,
∴當x∈[0,1]時,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函數,∴當x∈[-1,0]時,f(x)=f(-x)=-x+1,
當x∈[1,2]時,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)利用條件可設A、B的橫坐標分別為3-t,t+1,1≤t≤2,則|AB|=(t+1)-(3-t)=2t-2,然后運用坐標表示三角形的面積。
(1)∵f(x)是以2為周期的周期函數,當x∈[2,3]時,f(x)=x-1,
∴當x∈[0,1]時,f(x)=f(x+2)=(x+2)-1=x+1.
∵f(x)是偶函數,∴當x∈[-1,0]時,f(x)=f(-x)=-x+1,
當x∈[1,2]時,f(x)=f(x-2)=-(x-2)+1=-x+3.
(2)設A、B的橫坐標分別為3-t,t+1,1≤t≤2,則|AB|=(t+1)-(3-t)=2t-2,∴△ABC的面積為S=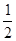 (2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-
(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-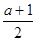 )2+
)2+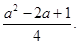
∵2<a<3,∴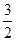 <
<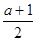 <2.當t=
<2.當t=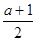 時,S最大值=
時,S最大值=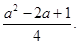


科目:高中數學 來源: 題型:
| π | 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年上海市金山區高三上學期期末考試數學試卷(解析版) 題型:解答題
(本題滿分12分,第1小題6分,第2小題6分)
已知集合A={x| | x–a | < 2,xÎR
},B={x| <1,xÎR }.
<1,xÎR }.
(1) 求A、B;
(2) 若 ,求實數a的取值范圍.
,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年安徽省高三10月月考理科數學試卷(解析版) 題型:解答題
(本題滿分12分)
設函數 (
( ,
, 為常數),且方程
為常數),且方程 有兩個實根為
有兩個實根為 .
.
(1)求 的解析式;
的解析式;
(2)證明:曲線 的圖像是一個中心對稱圖形,并求其對稱中心.
的圖像是一個中心對稱圖形,并求其對稱中心.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年重慶市高三第二次月考文科數學 題型:解答題
(本題滿分12分,(Ⅰ)小問4分,(Ⅱ)小問6分,(Ⅲ)小問2分.)
如圖所示,直二面角 中,四邊形
中,四邊形 是邊長為
是邊長為 的正方形,
的正方形, ,
, 為
為 上的點,且
上的點,且 ⊥平面
⊥平面
(Ⅰ)求證: ⊥平面
⊥平面
(Ⅱ)求二面角 的大小;
的大小;
(Ⅲ)求點 到平面
到平面 的距離.
的距離.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com