Question

已知中心在坐標原點的雙曲線C的右焦點為（2，0），右頂點為（3，0）.

（1）求雙曲線C的方程；

（2）求若直線l：y=kx+與雙曲線C恒有兩個不同的交點A和B，且＞2(其中O為原點)，求k的取值范圍；

（3）已知點M(,0),在（2）的條件下，求M到直線l的距離d的取值范圍.

Answer 1

思路分析：對于（1），可先設雙曲線C的方程，再由題意求出a,b的值；對于（2），為直線與雙曲線的交點問題，聯立方程，解方程組即可；（3）為點到直線的距離問題，代入點到直線的距離公式求解即可.

解：（1）設雙曲線方程為=1(a＞0,b＞0)，由已知得a=,c=2.

∴b=1.故所求雙曲線的方程為=1，即=1.

（2）將y=kx+代入=1，可得(1-3k²)x²--9=0.

由直線l：y=kx+與雙曲線C恒有兩個不同的交點，得

故k²≠且k²＜1.                                ①

設A(x₁,y₁),B(x₂,y₂)，則x₁+x₂=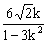,x₁x₂=.

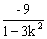由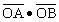＞2，得x₁x₂+y₁y₂＞2.

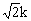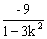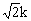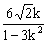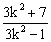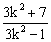而x₁x₂+y₁y₂=x₁x₂+(kx₁+)(kx₂+)=(k²+1)x₁x₂+(x₁+x₂)+2=(k²+1)·+·+2=,

∴＞2.

解此不等式,得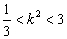.                       ②

由①②,得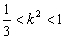.故k的取值范圍是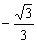(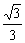-1,)∪(,1).

（3）點M到直線l的距離為d=.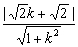

∴d²=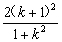=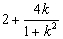,k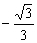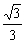∈(-1,)∪(,1)

設f(k)=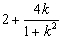,k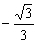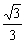∈(-1,)∪(,1),

則f′(k)=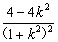. ∵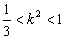,∴f′(k)＞0.

∴f(k)在區間(-1,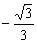)∪(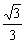,1)上均為增函數.

當k∈(-1,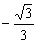)時，f(-1)＜f(k)＜f()，

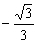即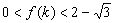.此時；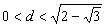

當k∈(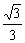,1)時，f(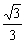)＜f(k)＜f(1)，

即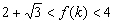.此時.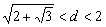

綜上所得M到直線l的距離d的取值范圍是(0,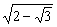)∪(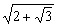,2).